Numerical solution methods

6.4. Numerical solution methods#

Systems of first-order ODEs can also be solved numerically using similar approaches as for single first-order ODEs, but now all dependent variables must be advanced simultaneously. The methods we use for single first-order ODES can be straightforwardly extended to systems using the explicit-form vector notation \(\vv{y}' = \vv{f}(t, \vv{y})\). For example, Euler’s method becomes:

(6.82)#\[\begin{equation} \vv{y}(t+\Delta t) \approx \vv{y}(t) + \vv{f}(t, \vv{y}) \Delta t \end{equation}\]

We are “just” adding columns to our calculations!

Example: First-order reaction in a draining tank

A first-order reaction (rate constant k) is taking place in a tank that is initially 1 M concentration in the reactant A and has 10 L of solution. A feed stream that has a reactant concentration of 1 M enters at 1 L / min, while well-mixed solution exits at 2 L / min.

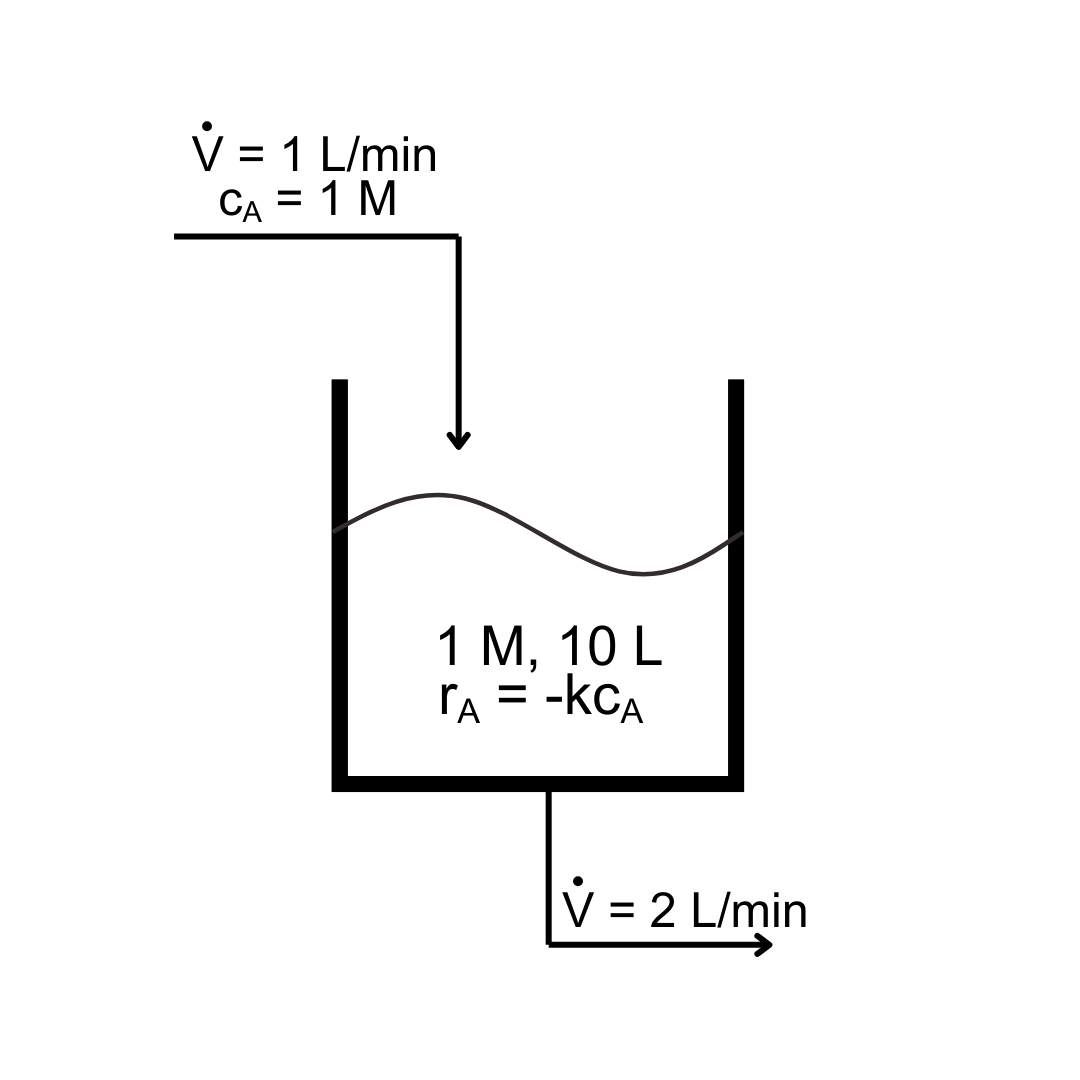
Reactions in draining tank.

Estimate the concentration of A after 1 minute if \(k = 0.5/{\rm min}\).

Start from an unsteady mole balance on A:

(6.83)#\[\begin{equation} \dd{}{n_{\rm A}}{t} = \dot n_{{\rm A},{\rm in}} - \dot n_{{\rm A},{\rm out}} + r_A V \end{equation}\]

The number of moles in the tank, the molar flow rate in, and the molar flow rate out are:

(6.84)#\[\begin{align} n_{\rm A} &= c_{\rm A} V \\ \dot n_{{\rm A},{\rm in}} &= c_{{\rm A},{\rm in}} \dot V_{\rm in} = 1 \\ \dot n_{{\rm A},{\rm out}} &= c_{\rm A} \dot V_{\rm out} = 2c_A \end{align}\]

so

(6.85)#\[\begin{align} \dd{}{(Vc_{\rm A})}{t} &= 1 - 2 c_A - k c_A V \\ V \dd{}{c_{\rm A}}{t} + c_{\rm A} \dd{}{V}{t} &= 1 - 2 c_A - k c_A V \end{align}\]

Since the volume V is changing, write a mass balance on the tank assuming that the solution density \(\rho\) does not depend on concentration:

(6.86)#\[\begin{align} \dd{}{m}{t} = \dot m_{\rm in} - \dot m_{\rm out} \end{align}\]

with the mass in the tank, mass flow rate in, and mass flow rate out:

(6.87)#\[\begin{align} m &= \rho V \\ \dot m_{\rm in} &= \rho \dot V_{\rm in} = \rho \\ \dot m_{\rm out} &= \rho \dot V_{\rm out} = 2 \rho \end{align}\]

so

(6.88)#\[\begin{align} \dd{}{(V\rho)}{t} = \rho \dd{}{V}{t} &= -\rho \\ \dd{}{V}{t} &= - 1 \end{align}\]

Substituting for \(\dd{}{V}{t}\) in the unsteady mole balance and rearranging gives the system of first-order ODES:

(6.89)#\[\begin{align} \dd{}{c_{\rm A}}{t} &= \frac{1}{V} \left(1 - c_A - 0.5Vc_A\right),& c_{\rm A}(0) &= 1 \\ \dd{}{V}{t} &= -1, & V(0) &= 10 \end{align}\]

Calling \(y_1 = c_{\rm A}\) and \(y_2 = V\):

\(n\)

\(t\)

\(y_1\)

\(y_2\)

\(f_1\)

\(f_2\)

0

0

1

10

-0.5

-1

1

0.2

0.9

9.8

-0.4398

-1

2

0.4

0.8120

9.6

-0.3864

-1

3

0.6

0.7347

9.4

-0.3389

-1

4

0.8

0.6669

9.2

-0.2972

-1

5

1.0

.6075

9

The concentration after 1 minute is approximately 0.6 M.

6.4.1. Skill builder problems#

  1. Determine \(y_1(5)\) and \(y_2(5)\) for

    (6.90)#\[\begin{align} y'_1 &= \frac{2}{3} y_1 - \frac{4}{3} y_1 y_2, & y(0) &= 1.5 \\ y'_2 &= y_1 y_2 - y_2, & y(0) &= 1 \end{align}\]

    using the Euler method with \(\Delta t = 0.5\).

    Solution

    The ODE is already in explicit form, so start solving from the initial condition.

    \(n\)

    \(t\)

    \(y_1\)

    \(y_2\)

    \(f_1\)

    \(f_2\)

    0

    0

    1.500

    1.000

    -1.000

    0.500

    1

    0.5

    1.000

    1.250

    -1.000

    0.000

    2

    1.0

    0.500

    1.250

    -0.500

    -0.625

    3

    1.5

    0.250

    0.938

    -0.146

    -0.703

    4

    2.0

    0.177

    0.586

    -0.020

    -0.482

    5

    2.5

    0.167

    0.345

    0.035

    -0.287

    6

    3.0

    0.184

    0.201

    0.073

    -0.164

    7

    3.5

    0.221

    0.120

    0.112

    -0.093

    8

    4.0

    0.277

    0.073

    0.158

    -0.053

    9

    4.5

    0.356

    0.046

    0.215

    -0.030

    10

    5.0

    0.464

    0.032

    The final result is \(y_1(5) = 0.464\) and \(y_2(5) = 0.032\).

Contents