1.1. Functions

A function is a rule that assigns a unique value \(f(x)\) to an input \(x\).

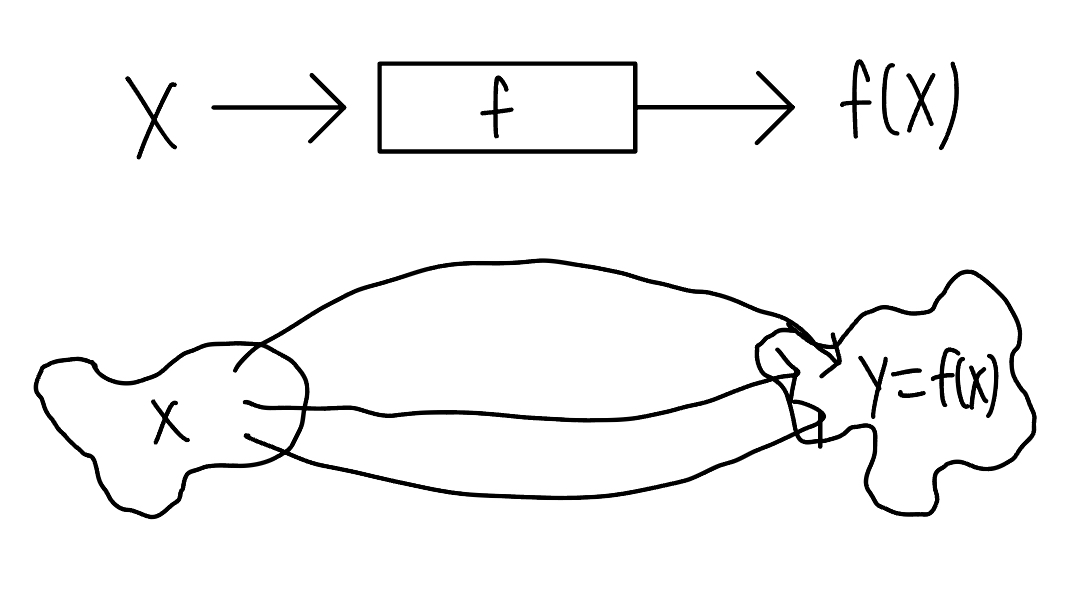
We call x the independent variable and \(y = f(x)\) the dependent variable. The domain of f is all possible values of x, while the range of f is all possible values of y.

A function can be represented by:

• An equation

  \[f(x) = x^2\]

• A table

  \(x\)	\(f\)
  0	0
  1	1
  2	4

• A graph:

  

• A description

  “Square x.”

Not all curves are functions! f must uniquely map x. For example, the circle \(x^2 + y^2 = 4\), or equivalently, \(y = \pm\sqrt{4-x^2}\) is not a function because one value of x can map to multiple values of y. Graphically, this fails the “vertical line test”:

Vertical line test

A vertical line cannot intersect a function twice.

1.1.1. Common functions

• Linear functions (lines)

  \[y = mx + b\]

  where m is the slope and b is the y-intercept.

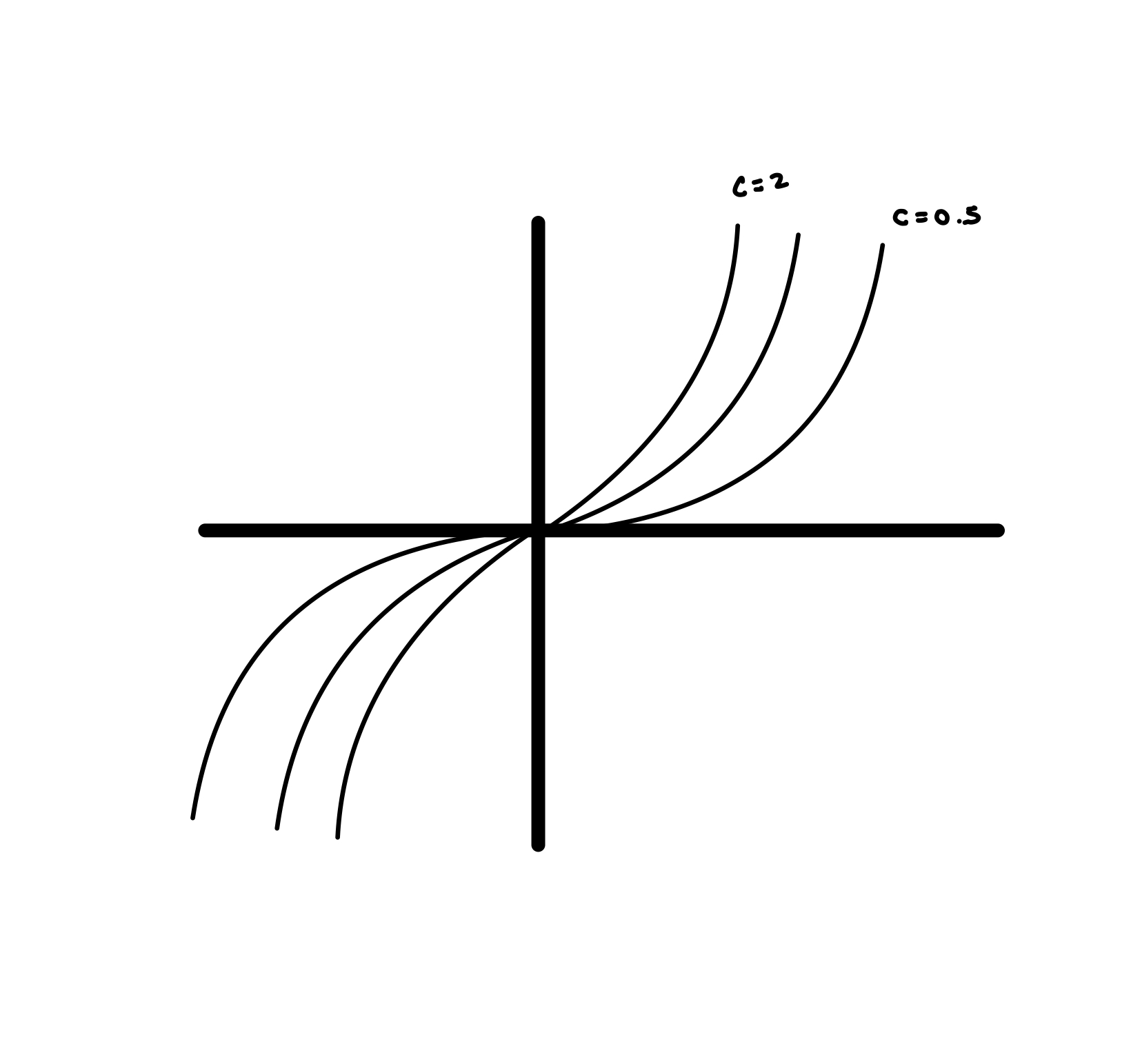
• Power functions (“power law”)

  \[y = kx^a\]

  where k is the prefactor and a is the power.

• Polynomials

  \[y = a_n x^n + \ldots + a_1x + a_0\]

  where n is the degree and \(a_i\) is the coefficient of the i-th power of x. The polynomial is quadratic when \(n=2\), cubic when \(n=3\), and quartic when \(n=4\).

• Exponential

  \[y = a^x\]

  where a is the base (\(a > 0\), \(a \ne 1\)). A special case is \(a = e\), Euler’s number (2.718…).

• Logarithmic

  \[y = \log_a x\]

  where a is the base (\(a > 0\), \(a \neq 1\)). Two special cases are \(a = e\), which we call the natural logarithm \(\ln\), and \(a = 10\), which we call the common logarithm, \(\log_{10}\).

• Trigonometric

  \[\begin{split} \sin x \qquad \csc x\\ \cos x \qquad \sec x\\ \tan x \qquad \cot x \end{split}\]

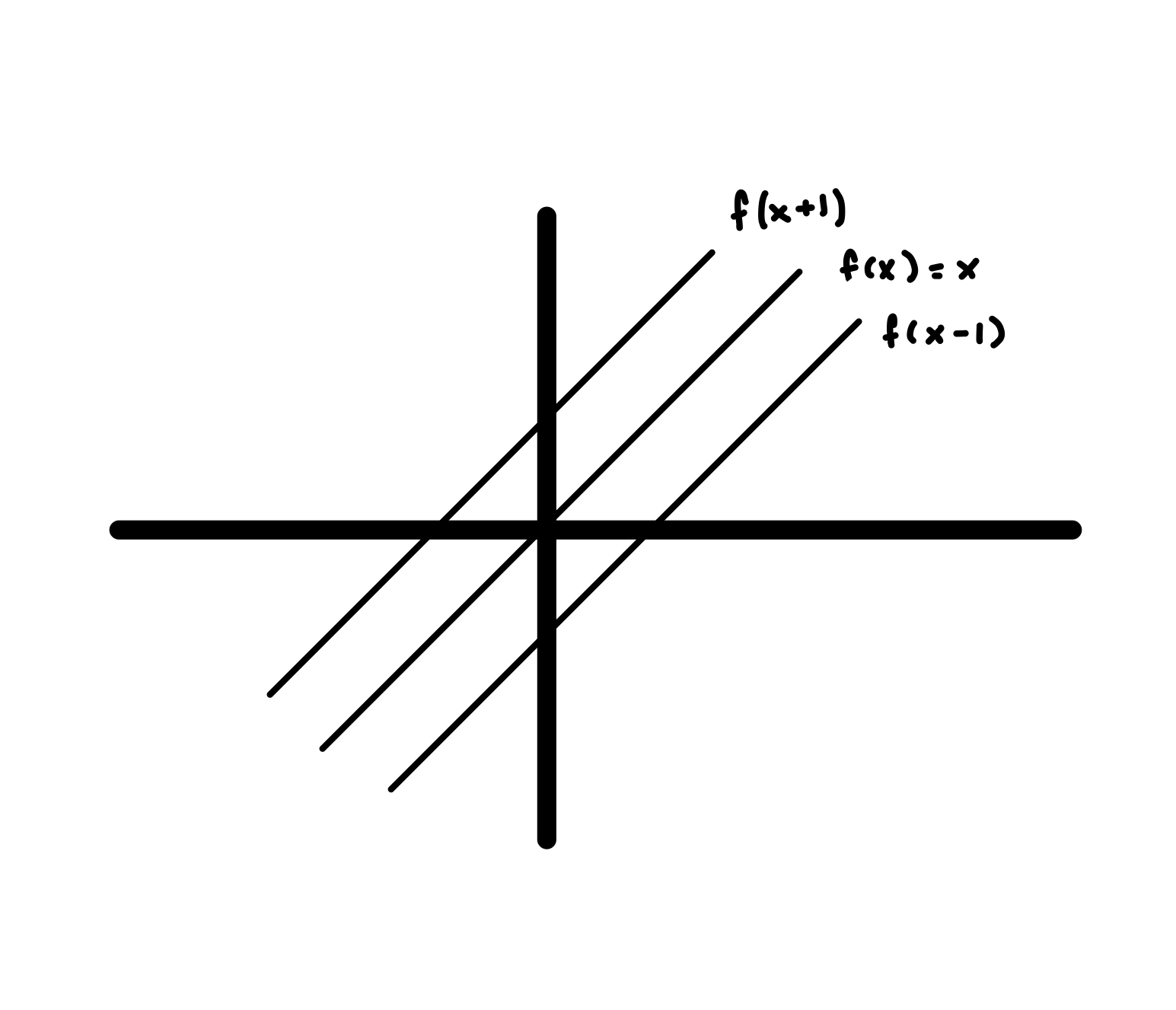
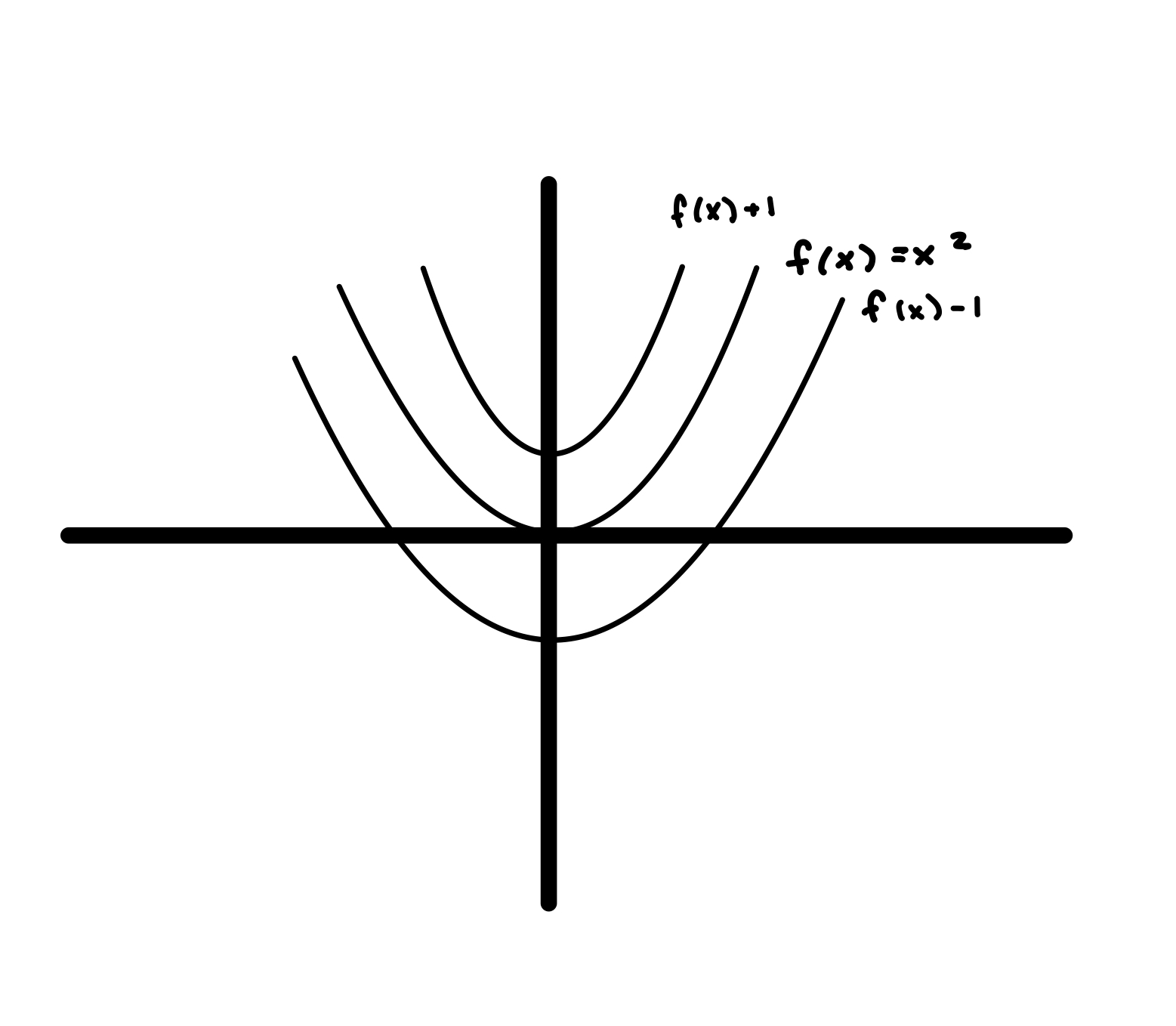
1.1.2. Manipulating functions

Horizontal shift

• \(f(x+a)\) shifts f left by a.

• \(f(x-a)\) shifts f right by a.

Vertical shift

• \(f(x)+b\) shifts f up by b.

• \(f(x)-b\) shifts f down by b.

Horizontal scaling

• Scaling \(f(cx)\) compresses f horizontally by c.

• Scaling \(f(x/c)\) stretches f horizontally by c.

Vertical scaling

• Scaling \(f(x)/c\) compresses f vertically by c.

• Scaling \(cf(x)\) streches f vertically by c.

1.1.3. Trigonometric functions

The given unit circle has a triangle drawn within which represents how trigonometric functions are related to lengths and heights of the sides of right triangles.

The circle has a radius and is centered at (0,0). A point on the circle is defined by angle \(\theta\) measured counterclockwise from the positive x-axis. Angles can be measured in degrees or radians:

(1.1)\[\begin{equation} \theta({\rm rad.}) = \theta({\rm deg.}) \left( \frac{\pi}{180^{\circ}} \right) \end{equation}\]

The trigonometric functions describe how the coordinates of a point on the unit circle relate to the angle \(\theta\):

(1.2)\[\begin{align} \sin(\theta)& = \frac{y}{r}& \cos(\theta)& = \frac{x}{r}& \tan(\theta)& = \frac{y}{x}\\ \csc(\theta)& = \frac{r}{y}& \sec(\theta)& = \frac{r}{x}& \cot(\theta)& = \frac{x}{y}\\ \end{align}\]

Each quadrant of the unit circle corresponds to a positive trigonometric function: All, Sine, Tangent, and Cosine.

Tip

A mnemonic to remember this order is “All Students Take Calculus”.

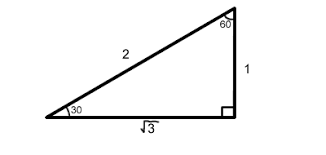
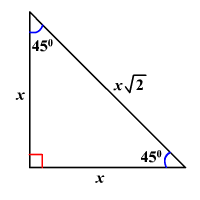
1.1.3.1. Special angles

30-60-90 triangle

A right triangle with \(30^\circ\) (\(\pi/6\)) and \(60^\circ\) (\(\pi/3\)) angles has the following side lengths:

45-45-90 triangle

A right triangle with \(45^\circ\) (\(\pi/4\)) angles has the following side lengths:

and so

\(\theta\)		\(\sin \theta\)	\(\cos \theta\)
\(30^\circ\)	\(\pi/6\)	\(1/2\)	\(\sqrt{3}/2\)
\(45^\circ\)	\(\pi/4\)	\(1/\sqrt{2}\)	\(1/\sqrt{2}\)
\(60^\circ\)	\(\pi/3\)	\(\sqrt{3}/2\)	\(1/2\)

What about angles greater than \(90^\circ\)? Take the angle of \(\theta\) relative to the x-axis, then apply the sign based on which quadrant the angle falls in.

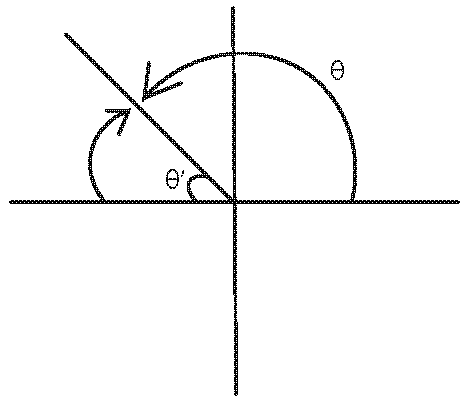
For example, if \(\theta = 135^\circ = 3\pi/4\), then the angle relative to the x-axis is \(\theta' = 45^\circ = \pi/4\). Hence,

(1.3)\[\begin{align} \sin \theta' &= \frac{1}{\sqrt{2}} & \cos \theta' &= \frac{1}{\sqrt{2}} \\ \sin \theta &= \frac{1}{\sqrt{2}} & \cos \theta &= -\frac{1}{\sqrt{2}} \end{align}\]

1.1.3.2. Physical meaning

In addition to their geometric significance, trigonometric functions typically represent physical waves.

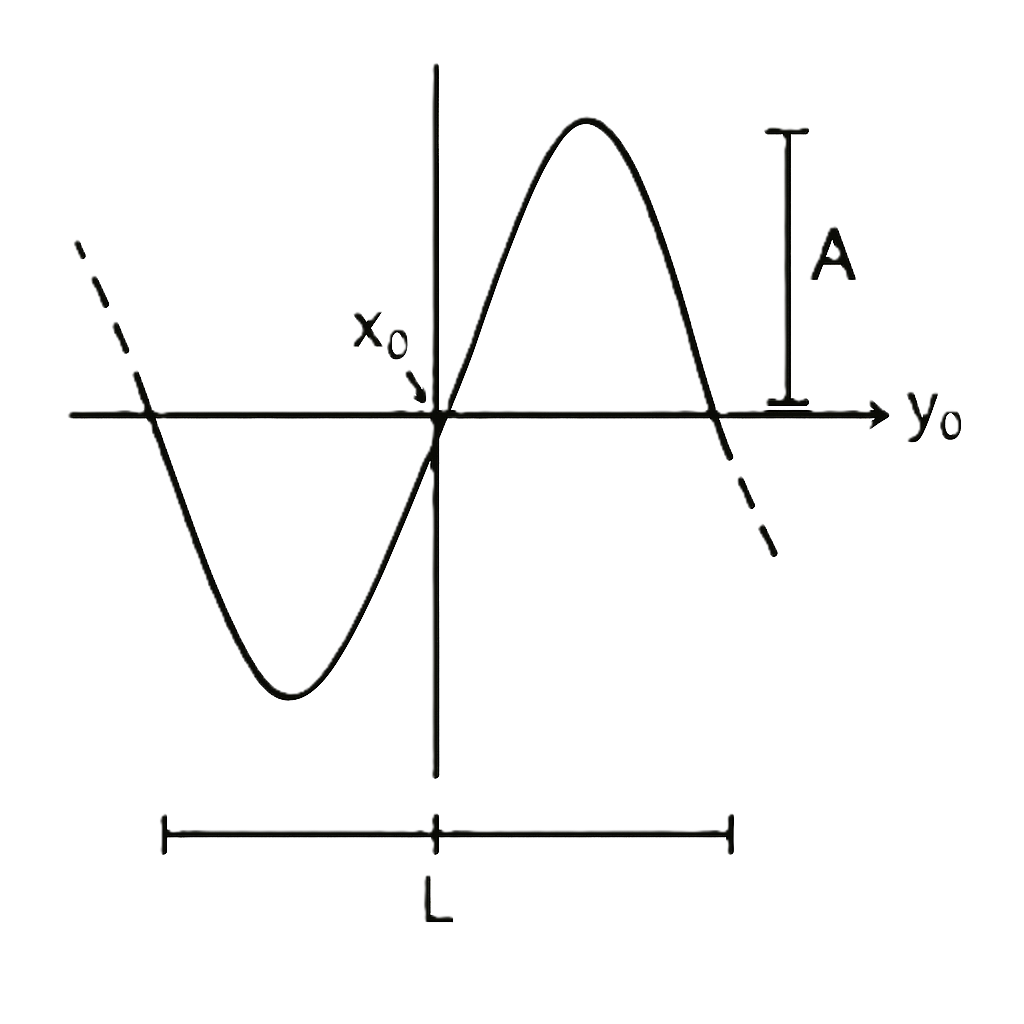
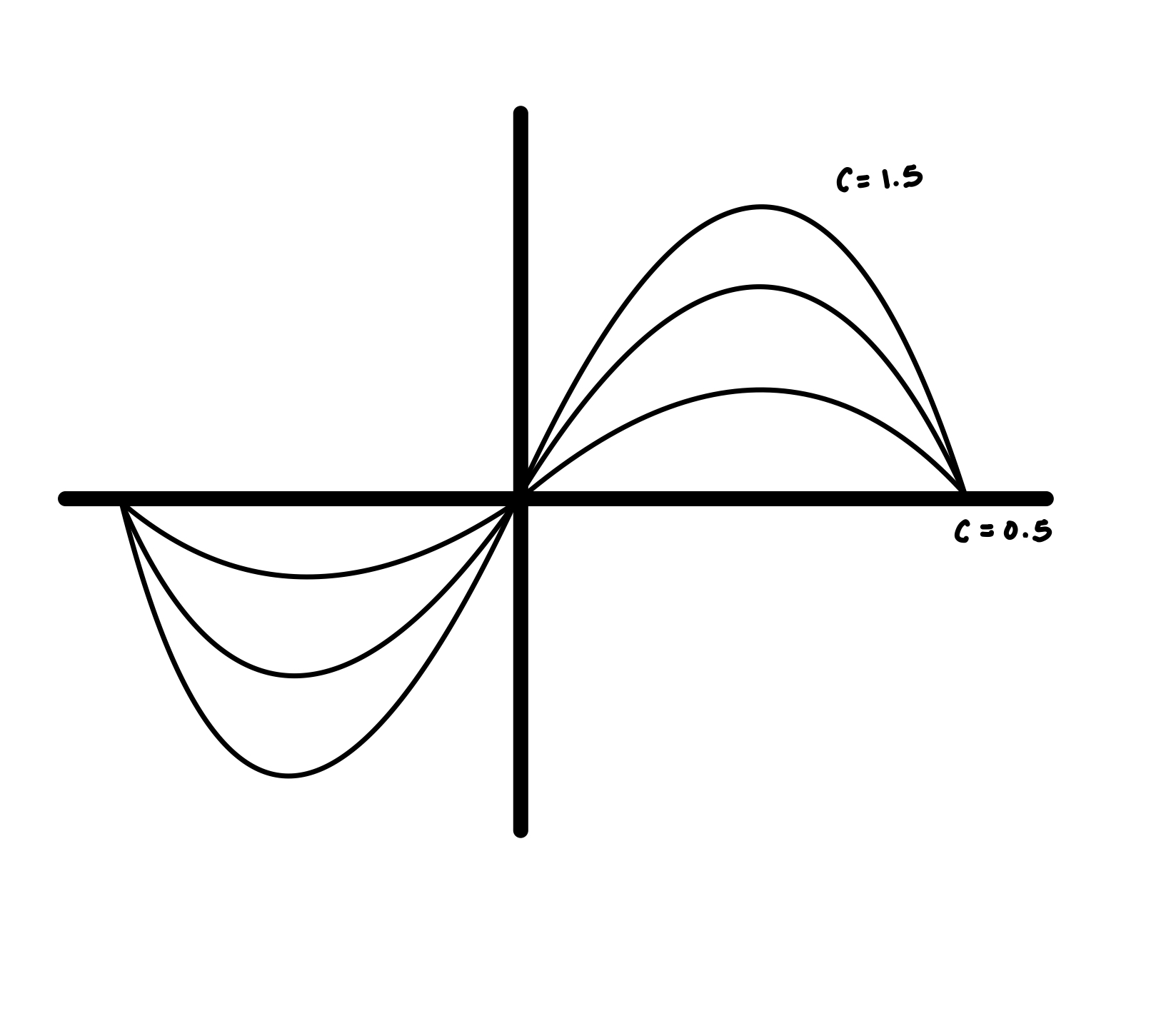
The properties of the wave can be encoded by manipulating the function.

(1.4)\[\begin{equation} y = A\sin\left[ \frac{2\pi}{L}(x + x_0) \right] + y_0 \end{equation}\]

where A is the amplitude of the wave, L is the period of the wave, \(x_0\) is a horizontal (phase) shift, and \(y_0\) is a vertical shift.