Numerical solution methods

7.7. Numerical solution methods#

7.7.1. Initial value problems#

We learned previously how to solve systems of first-order ODEs:

(7.179)#\[\begin{equation} \vv{y}' = \vv{f}(t, \vv{y}) \end{equation}\]

using Euler’s method. However, we didn’t learn what to do with higher-order derivatives. If a second-order ODE can be written in explicit form and as an initial value problem:

(7.180)#\[\begin{equation} y'' = f(t, y, y'), \quad y(0) = y_0, \quad y'(0) = y_0' \end{equation}\]

it can be solved by conversion to a system of first-order ODEs!

Let’s verify this works using an ODE that we can solve analytically. Consider:

(7.182)#\[\begin{equation} y'' + y' - 2y = 0 \quad y(0) = 4, \quad y'(0) = -5 \end{equation}\]

We previously showed using the characteristic polynomial that the solution to this IVP is:

(7.183)#\[\begin{equation} y = e^x + 3e^{-2x} \end{equation}\]

Now, let’s resolve by converting to a system. Let \(y_1 = y\) and \(y_2 = y'\). Then, the ODE is equivalent to

(7.184)#\[\begin{align} y'' &= 2y - y' \\ y_2' &= 2y_1 - y_2 \end{align}\]

and the system of ODEs is:

(7.185)#\[\begin{align} y_1' &= y_2, & y_1(0) &= 4 \\ y_2' &= 2y_1 + -y_2, & y_2(0) &= -5 \end{align}\]

This system of ODES is in the form \(\vv{y}' = \vv{A}\vv{y}\) with

(7.186)#\[\begin{equation} \begin{bmatrix} 0 & 1 \\ 2 & -1\end{bmatrix} \end{equation}\]

The eigenvalues of the matrix are

(7.187)#\[\begin{align} |\vv{A}-\lambda \vv{I}| &=\begin{vmatrix}-\lambda & 1\\ 2& -1-\lambda \end{vmatrix} \\ &=\lambda(\lambda+1)-2 \\ &= \lambda^2 + \lambda - 2 \\ &= (\lambda-1)(\lambda+2) = 0 \end{align}\]

giving \(\lambda_1 = 1\) and \(\lambda_2 = -2\). The corresponding eigenvectors are:

(7.188)#\[\begin{align} \vv{A} - \lambda_1 \vv{I} &= \begin{bmatrix} -1 & 1 \\ 2 & -2 \end{bmatrix} \to \vv{x}_1 = \begin{bmatrix}1 \\ 1\end{bmatrix} \\ \vv{A} - \lambda_2 \vv{I} &= \begin{bmatrix} 2 & 1 \\ 2 & 1 \end{bmatrix} \to \vv{x}_2 = \begin{bmatrix}1 \\ -2\end{bmatrix} \end{align}\]

Hence,

(7.189)#\[\begin{equation} \vv{y} = c_1 e^x \begin{bmatrix}1 \\ 1\end{bmatrix} + c_2 e^{-2x} \begin{bmatrix}1 \\ -2\end{bmatrix} \end{equation}\]

Apply the initial conditions by solving \(\vv{X} \vv{c} = \vv{y}(0)\)

(7.190)#\[\begin{align} \begin{bmatrix}1 & 1 & 4 \\ 1 & -2 & -5 \end{bmatrix} \begin{matrix}\vphantom{R_1} \\ -R_1\end{matrix} &\to \begin{bmatrix}1 & 1 & 4 \\ 0 & -3 & -9 \end{bmatrix} \begin{matrix}\vphantom{R_1} \\ \div -3\end{matrix} \\ &\to \begin{bmatrix}1 & 1 & 4 \\ 0 & 1 & 3 \end{bmatrix} \begin{matrix} -R_2 \\ \vphantom{R_2}\end{matrix} \\ &\to \begin{bmatrix}1 & 0 & 1 \\ 0 & 1 & 3 \end{bmatrix} \end{align}\]

so

(7.191)#\[\begin{equation} \vv{y} = e^x \begin{bmatrix}1 \\ 1\end{bmatrix} + 3 e^{-2x} \begin{bmatrix}1 \\ -2\end{bmatrix} \end{equation}\]

or equivalently

(7.192)#\[\begin{equation} y = y_1 = e^x + 3 e^{-2x} \end{equation}\]

The solution is the same as before! Note that in the process, we also obtained

(7.193)#\[\begin{equation} y' = y_2 = e^x - 6 e^{-2x} \end{equation}\]

which is consistent with direct differentiation of \(y\).

Example: Forced oscillator

A mass m on a Hookean spring (constant k) is experiences both a drag force (friction coefficient \(\gamma\)) and an oscillating external force \(F \cos \omega t\). Its position x obeys the differential equation

(7.194)#\[\begin{equation} m x'' + \gamma x' + kx = F \cos\omega t, \quad x(0) = x_0, \quad x'(0) = v_0 \end{equation}\]

where \(x_0\) and \(v_0\) are the initial position and velocity of the mass. Write this second-order ODE as a system of first-order ODEs.

Let \(y_1 = x\) and \(y_2 = x'\). Then, the ODE is equivalent to:

(7.195)#\[\begin{align} x'' = \frac{1}{m}\left(- kx - \gamma x' + F\cos\omega t\right) \\ y_2' = \frac{1}{m}\left(- k y_1 - \gamma y_2 + F\cos \omega t \right) \end{align}\]

so

(7.196)#\[\begin{align} y_1' &= y_2, & y_1(0) &= x_0 \\ y_2' &= \displaystyle \frac{1}{m}\left(-\gamma y_2 - k y_1 + F\cos \omega t \right), & y_2(0) &= v_0 \end{align}\]

7.7.2. Boundary value problems#

We can solve initial value problems for second-order ODEs by converting to a system and using methods we know. What about boundary value problems?

Let’s say we want to solve:

(7.197)#\[\begin{equation} y'' + y = 0, \quad y(0) = 0, \quad y(\pi/6) = 4 \end{equation}\]

Using normal approach:

(7.198)#\[\begin{align} y &= c_1 \cos x + c_2 \sin x \\ y(0) &= c_1 = 0\\ y(\pi/6) &= c_2 \frac{1}{2} = 4 \to c_2 = 8\\ \end{align}\]

so,

(7.199)#\[\begin{equation} y = 8 \sin x \end{equation}\]

What if we needed to do this numerically? Try converting to system using \(y_1 = y\) and \(y_2 = y'\), so

(7.200)#\[\begin{equation} y'' + y = 0 \to y_2' = -y_1 \end{equation}\]

and

(7.201)#\[\begin{align} y_1' &= y_2, & y_1(0) &= 0 \\ y_2' &= -y_1, & y_2(0) &= a \end{align}\]

where a is an unknown value that we need to figure out so that \(y(\pi/6) = 4\).

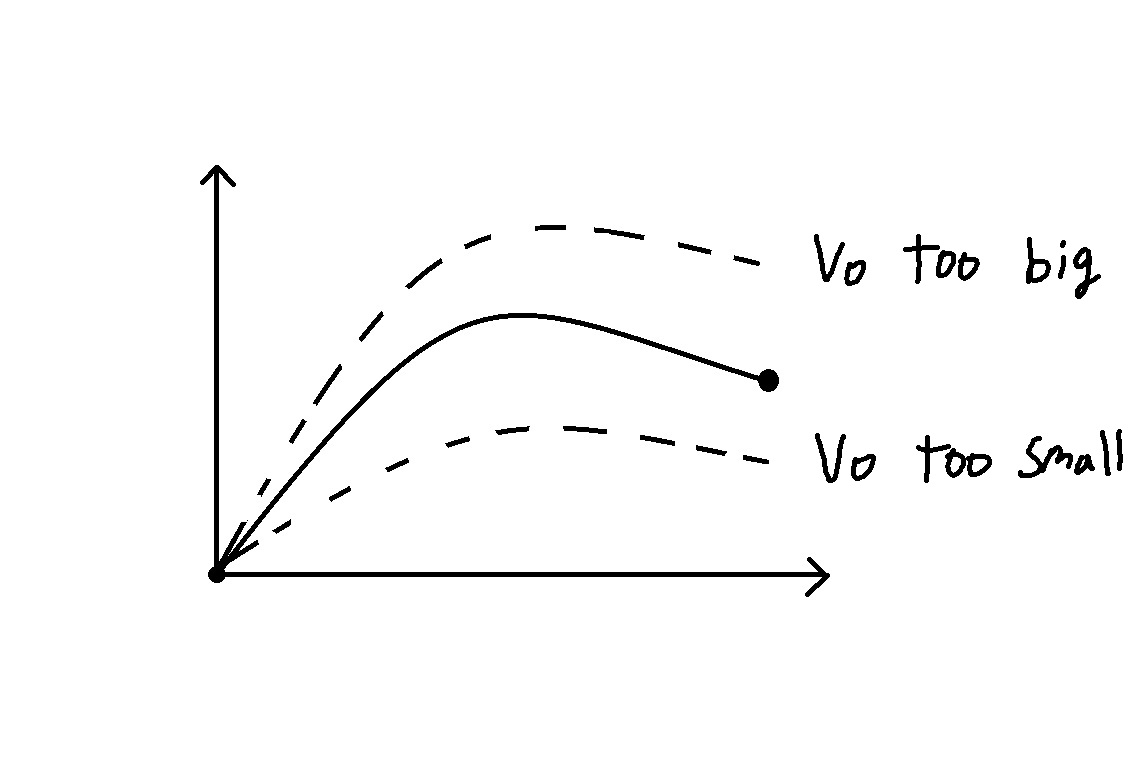
We will use the shooting method to determine a. The idea is to treat the boundary condition at the other value of x as a function of a, then vary a using a root-finding approach.

Graph of Lines

This boundary-condition function is the numerical integration of the system of ODEs! Bisection search is well-suited for solving for a because it is stable and doesn’t require a derivative.

Example: Reaction-diffusion with second-order reaction

We are solving a reaction-diffusion problem with a second-order reaction:

(7.202)#\[\begin{equation} D \dd{2}{c}{x} - k c^2 = 0, \quad c(0) = c_0, \quad -D c'(L) = 0 \end{equation}\]

Formulate in a form suitable for numerical solution using the shooting method.

First, rewrite as a system of first-order ODEs using \(y_1 = c\) and \(c_2 = c'\). The ODE is

(7.203)#\[\begin{equation} c'' - \frac{k}{D}c^2 \to y_2' = \frac{k}{D} y_1^2 \end{equation}\]

so

(7.204)#\[\begin{align} y_1' &= y_2, & y_1(0) &= c_0 \\ y_2' &= \frac{k}{D} y_1, & y_2(0) &= a \end{align}\]

where a is the unknown value of \(y_2(0)\). Vary a until

(7.205)#\[\begin{equation} -D c'(L) = 0 \to y_2(L) = 0 \end{equation}\]
Contents