Substitution

7.1. Substitution#

Some second-order ODEs can be solved by making a substitution

(7.1)#\[\begin{equation} u = \dd{}{y}{x} \end{equation}\]

Then, you effectively “integrate twice”: once to solve for u, then once more to get y from u.

Example: Kinematics

Newton’s second law is \(F = ma\), where F is the applied force, m is the mass, and a is the acceleration of a body. We also know that acceleration is the derivative of the velocity v, which is itself the first derivative of position x. Hence, Newton’s second-law is a second-order ODE:

(7.2)#\[\begin{equation} m \dd{2}{x}{t} = F \end{equation}\]

Solve for the position of a body x as a function of time t experience a constant gravitational force \(F = -mg\), where g is the acceleration due to gravity.

Substitute the gravitational force and simplify

(7.3)#\[\begin{align} m \dd{2}{x}{t} &= -mg \\ \dd{2}{x}{t} &= -g \end{align}\]

Make the substitution \(v = \d{x}/\d{t}\), then integrate because the ODE is separable

(7.4)#\[\begin{align} \dd{}{v}{t} &= -g \\ \int \d{v} &= \int -g \d{t} \\ v &= -g t + c_1 \end{align}\]

Replace v and integrate again:

(7.5)#\[\begin{align} \dd{}{x}{t} &= -g t + c_1 \\ \int \d{x} &= \int\left(-g t + c_1 \right)\d{t} \\ x &= -\frac{1}{2} g t^2 + c_1 t + c_2 \end{align}\]

If the initial position is \(x(0) = x_0\) and initial velocity is \(v(0)=x'(0)=v_0\), then

(7.6)#\[\begin{align} x(0) &= c_2 = x_0 \\ v(0) &= c_1 = v_0 \end{align}\]

so

(7.7)#\[\begin{equation} x(t) = -\frac{1}{2} g t^2 + v_0 t + x_0 \end{equation}\]

This is the classic equation of ballistic motion!

Example: Incompressible flow in a cylinder

Steady, laminar pressure-driven flow in a cylindrical pipe:

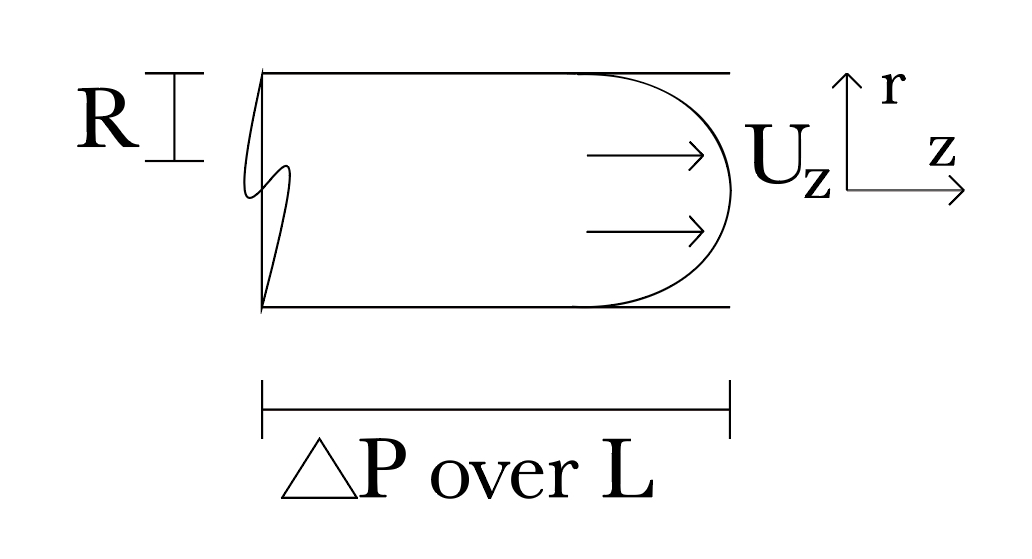
Pipe flow

is governed by the simplified Navier-Stokes equation:

(7.8)#\[\begin{equation} \mu \frac{1}{r} \dd{}{}{r} \left( r \dd{}{u_z}{r} \right) = -\frac{\Delta P}{L} \end{equation}\]

where \(u_z\) is the velocity along the pipe axis, \(\Delta P\) is the difference between the pressure at the inlet and at the outlet, L is the length of the pipe, and \(\mu\) is the dynamic viscosity.

The pipe walls have no-slip boundary conditions, meaning the velocity is zero there. Derive an expression for \(u_z(r)\).

Make the substitution \(v = r \d{u_z}/\d{r}\), then rearrangeso

(7.9)#\[\begin{align} \mu \frac{1}{r} \dd{}{v}{r} &= -\frac{\Delta P}{\mu L} \\ \int \d{v} &= \int -\frac{1}{\mu} \frac{\Delta P}{L} r \d{r} \\ v &= -\frac{1}{2\mu} \frac{\Delta P}{L} r^2 + c_1 \end{align}\]

Then, substitute for v, separate, and integrate again:

(7.10)#\[\begin{align} r \dd{}{u_z}{r} &= -\frac{1}{2\mu} \frac{\Delta P}{L} r^2 + c_1 \\ \int \d{u_z} &= \int \Biggl( -\frac{1}{2\mu} \frac{\Delta P}{L} r + \frac{c_1}{r} \Biggr) \d{r} \\ u_z &= -\frac{1}{4\mu} \frac{\Delta P}{L} r^2 + c_1 \ln r + c_2 \end{align}\]

The walls have no-slip boundary conditions so \(u_z(R) = 0\). Additionally, the pipe must have radial symmetry so \(u_z'(0) = 0\). Applying these boundary conditions requires:

(7.11)#\[\begin{align} \lim_{r \to 0} u_z'(r) &= \lim_{r \to 0} \frac{c_1}{r} = 0 \\ u_z(R) &= -\frac{1}{4\mu} \frac{\Delta P}{L} R^2 + c_1 \ln R + c_2 = 0 \end{align}\]

The first equation requires \(c_1 = 0\). The second equation then gives

(7.12)#\[\begin{equation} c_2 = \frac{1}{4\mu} \frac{\Delta P}{L} R^2 \end{equation}\]

All together,

(7.13)#\[\begin{equation} u_z(r)=\frac{1}{4 \mu}\frac{\Delta P}{L}(R^2-r^2) \end{equation}\]

This is the classic Hagen-Poiseuille flow profile.