Derivatives

1.4. Derivatives#

1.4.1. Tangent line and rate of change#

A tangent line touches a curve exactly once.

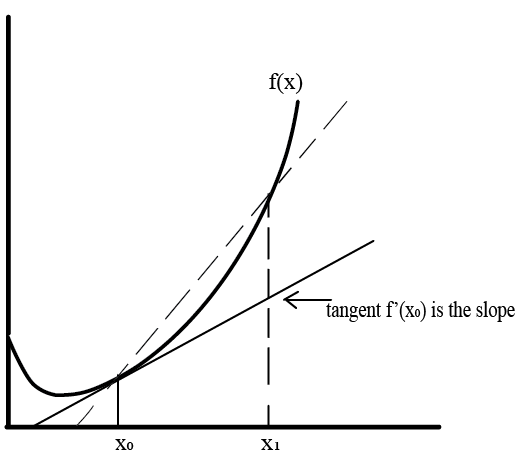
How can we estimate the slope of the line at \(x_0\)? First, evaluate \(f(x_0)\). Then, evaluate \(f(x_1)\) at another point nearby. The slope is:

(1.59)#\[\begin{equation} \frac{f(x_1)-f(x_0)}{x_1-x_0} \end{equation}\]

If we make \(x_1\) very close to \(x_0\), we will get the slope of the tangent line. This suggests uses of a limit! We call the slope of the tangent to f at \(x\) the derivative of f.

The derivative represents how fast the function is changing (rate of change). This is especially useful in physics when the function represents a coordinate, and the independent variable is time.

Example: Ball moving with constant velocity

A ball has position coordinate x and is moving with constant velocity v, so

(1.61)#\[\begin{equation} x(t) = x_0 + vt \end{equation}\]

where \(x_0\) is the initial position that it starts from.

Show that the first derivative of the position x is the velocity v.

(1.62)#\[\begin{align} x'(t) &= \lim_{h\to 0} \frac{x(t+h)-x(t)}{h} \\ &= \lim_{h\to 0} \frac{[x_0+v(t+h)]-[x_0+vt]}{h} \\ &=\lim_{h\to 0} \frac{vh}{h} \\ &= v \end{align}\]

1.4.2. Formal definition#

The derivative is also a function!

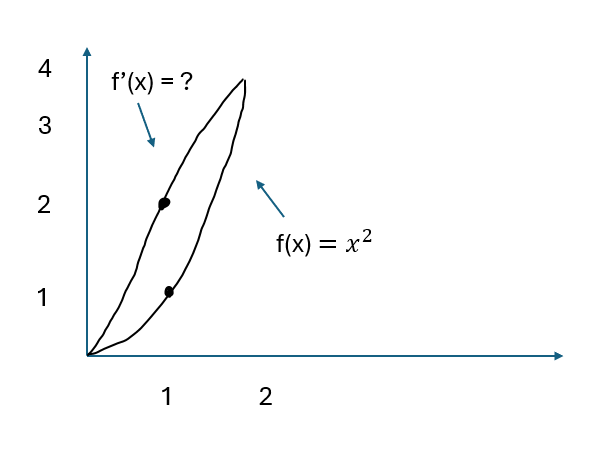
For example, if \(f(x) = x^2\),

(1.63)#\[\begin{align} f'(x) &= \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} \\ &= \lim_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} \\ &= \lim_{h \to 0} \frac{2xh + h^2}{h} \\ &= \lim_{h \to 0} (2x + h) \\ &= 2x \end{align}\]

This function represents how the slope of the line tangent to f is changing with x. For this function, the slope continually increases! Some additional examples:

\(f(x) = (x - 1)^2 + 1\)

Solution

(1.64)#\[\begin{align} f'(x) &= \lim_{h \to 0} \frac{[(x + h - 1)^2 + 1] - [(x - 1)^2 + 1]}{h} \\ &= \lim_{h \to 0} \frac{(x - 1)^2 + 2(x - 1)h + h^2 + 1 - (x - 1)^2 - 1}{h} \\ &= \lim_{h \to 0} \frac{2(x - 1)h + h^2}{h} \\ &= \lim_{h \to 0} 2(x - 1) + h \\ &= 2(x - 1) \end{align}\]
\(f(x) = 1/x\)

Solution

(1.65)#\[\begin{align} f'(x) &= \lim_{h \to 0} \frac{\dfrac{1}{x+h} - \dfrac{1}{x}}{h} \\ &= \lim_{h \to 0} \frac{\dfrac{x - (x + h)}{x(x+h)}}{h} \\ &= \lim_{h \to 0} \frac{\dfrac{- h}{x(x+h)}}{h} \\ &= \lim_{h \to 0} \frac{-1}{(x+h)x} \\ &= \frac{-1}{x^2} \end{align}\]

1.4.3. Differentiability#

To be differentiable, this limit must exist. A function would not be differentiable at a jump, cusp, coner, or vertical tangent

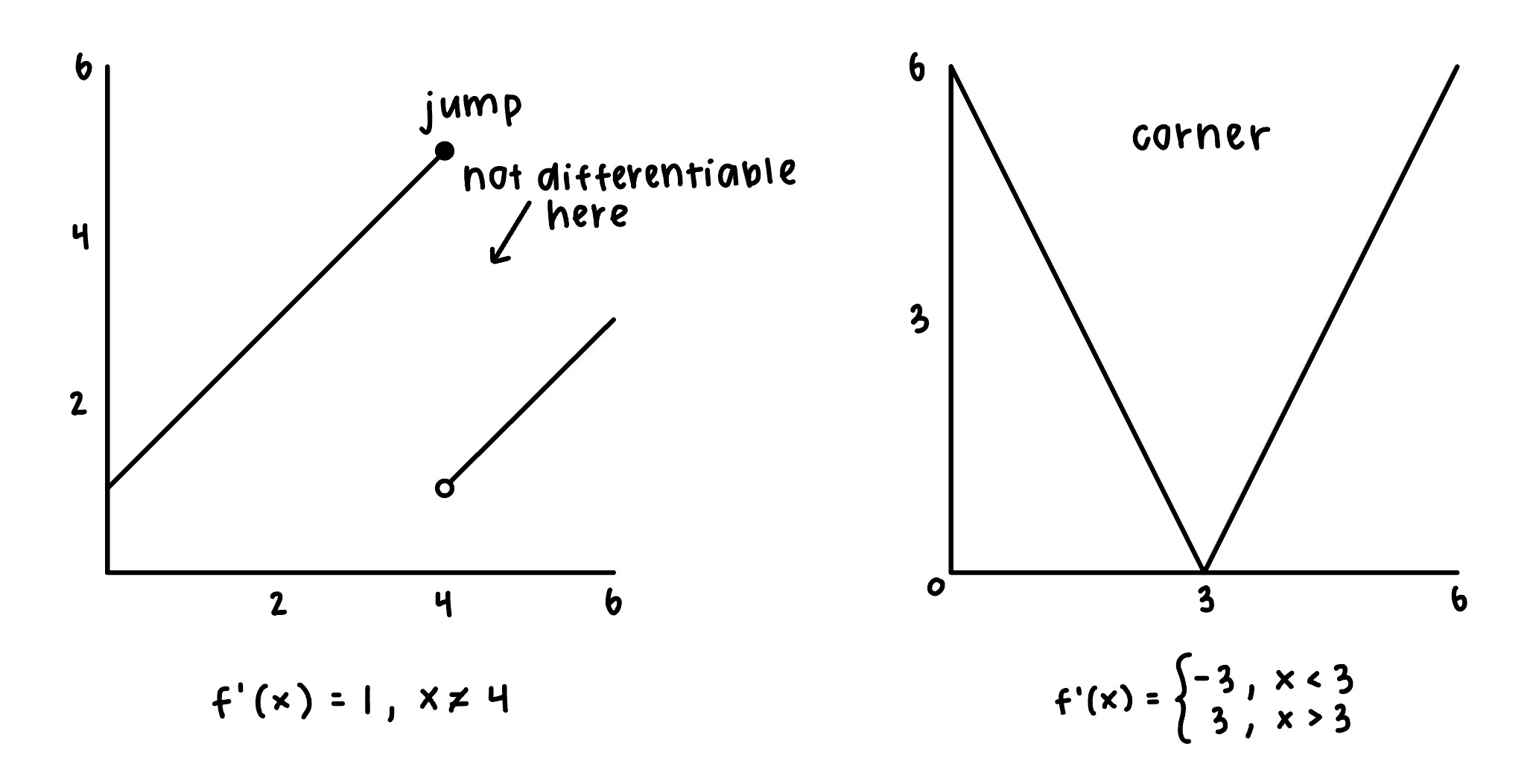
1.4.4. Higher-order derivatives#

We can try to take the derivative of any function, including the derivative itself! For example, consider \(f(x) = x^2\), which has \(f'(x) = 2x\). We can evaluate the derivative of \(f'\), which we will denote \(f''\) using the same formal definition:

(1.66)#\[\begin{align} f''(x) &= \lim_{h \to 0}{\frac{f'(x+h)-f'(x)}{h}} \\ &= \lim_{h \to 0}{\frac{2(x+h)-2x}{h}} \\ &= \lim_{h \to 0}{\frac{2h}{2}} \\ &= 2 \end{align}\]

We call \(f''\) the second derivative of f. Repeating the process we can obtain even higher-order derivatives. These may be denoted by additional primes (e.g., \(f'''\)), but often by a superscript (e.g., \(f^{(3)}\)) since it gets clunky to count too many primes.

Higher-order derivatives tell us about how lower-order derivatives are changing. For example, the second derivative tells us how the first derivative changes.

In a physical setting, we may have names for these different derivatives. For example, if we have the position x, the velocity v is the first derivative of x, while the acceleration a is the first derivative of v and second derivative of x.

Position	Velocity	Acceleration
x	x’	x’’
	v	v’
		a

Example: Ballistic motion

Consider the two-dimensional ballistic motion:

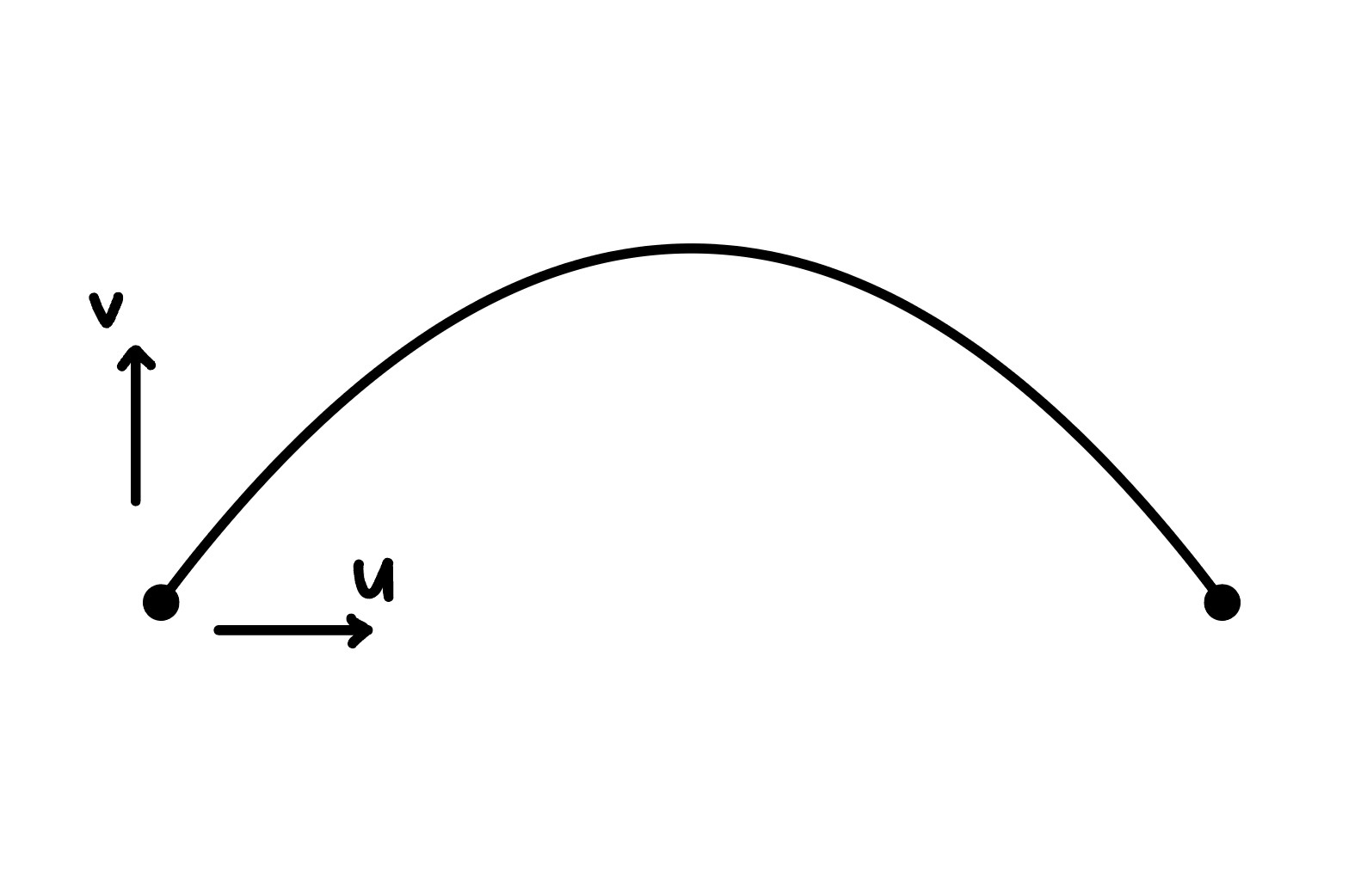
The equations of motion for the horizontal position x and vertical position y are:

(1.67)#\[\begin{align} x(t) &= u_0 t & \\ y(t) &= v_0 t - \frac{1}{2} g t^2 \end{align}\]

where \(u_0\) and \(v_0\) are the initial x and y components of the velocity, and g is the acceleration due to gravity. Find the velocity and acceleration in x and y.

In the x direction, call the velocity u. Then,

(1.68)#\[\begin{equation} u = x' = u_0 \end{equation}\]

Since u is a constant, the first derivative of u (second derivative of x) must be zero, and there is no acceleration in the x direction.

In the y direction, call the velocity v. Then,

(1.69)#\[\begin{align} v &= y' = v_0 - gt \\ a &= v' = y'' = -g \end{align}\]

The velocity in y is constantly increasing from the constant acceleration a due to gravity. This makes sense from what we know from physics!