Separable differential equations

5.2. Separable differential equations#

For example, to solve \(y' = xy\), separate the variables and integrate:

(5.11)#\[\begin{align} \int \frac{\d{y}}{y} &= \int x \d{x} \\ \ln y &= \frac{x^2}{2} + c_0 \\ y &= e^{x^2/2 + c_0} \\ y &= c e^\frac{x^2}{2} \end{align}\]

Note that here, we are being careful to denote the redefinition of the integration constant (\(c = e^{c_0}\)). This detail may be glossed over at times.

Example: Chemical reaction kinetics

A substance is disappearing according to a first-order reaction, so its concentration follows

(5.12)#\[\begin{equation} \dd{}{c}{t} = -k c \end{equation}\]

where \(k\) is the reaction rate constant. If the initial concentration of the reactant was 1.0 M and the concentration after 1 hour has passed is 0.70 M, what is the reaction rate constant?

First, solve the differential equation using separation of variables

(5.13)#\[\begin{align} \int \frac{1}{c} \d{c} &= \int -k \d{t} \\ \ln c &= -k t + B \end{align}\]

where B is an unknown integration constant. Apply the initial condition that \(c(0) = 1\)

(5.14)#\[\begin{equation} \ln 1 = -k \cdot 0 + B \to B = 0 \end{equation}\]

Hence,

(5.15)#\[\begin{equation} k = -\frac{\ln c}{t} \end{equation}\]

We know that \(c(1) = 0.70\) so

(5.16)#\[\begin{equation} k = -\frac{\ln 0.7}{1\,{\rm h}} = 0.36\,{\rm h}^{-1} \end{equation}\]

Example: Newton’s law of cooling

Estimate the temperature T in an office building at 6 a.m. if the heat goes off at 10 p.m. when the building is 70°F and the outside temperature \(T_\infty\) is 45°F if the T follows

(5.17)#\[\begin{equation} \dd{}{T}{t} = -k(T - T_\infty) \end{equation}\]

where \(k = 0.05\,{\rm h}^{-1}\).

Separate the differential equation and integrate

(5.18)#\[\begin{align} \int \frac{1}{T - T_\infty} \d{T} &= \int -k \d{t} \\ \ln(T - T_\infty) &= -kt + c \\ T - T_\infty &= C e^{-kt} \\ T &= T_\infty + C e^{-kt} \end{align}\]

Call 10 p.m. the time where \(t = 0\). Then,

(5.19)#\[\begin{equation} 70 = T(0) = 45 + C \to C = 25 \end{equation}\]

Last, evaluate the temperature at 6 a.m. when \(t = 8\):

(5.20)#\[\begin{equation} T(8) = 45 + 25 e^{-0.05 \cdot 8} = 62 \end{equation}\]

The temperature is approximately 62°F.

Example: Toricelli’s Law

A 1 cm hole opens at the bottom of a 1 m cylindrical tank. Water exits the hole with velocity that follows Toricelli’s, \(\sqrt{2gh}\) where g is the acceleration due to gravity and g is the height of water above the hole.

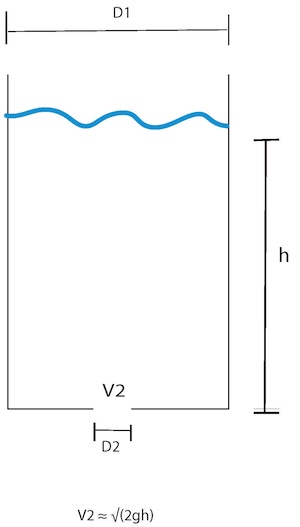
Tank draining through a pinhole

If there is 2 m of water in the tank initially, when does it drain?

Start from the unsteady balance on the mass of water m in the tank

(5.21)#\[\begin{equation} \dd{}{m}{t} = -\dot m_{\rm out} \end{equation}\]

The mass of water is

(5.22)#\[\begin{equation} m = \rho V = \rho \frac{\pi D_1^2}{4} h \end{equation}\]

where \(\rho\) is the density of water, V is the volume of water in the tank, and \(D_1\) = 1 m is the diameter of the tank. V is replaced using the volume of a cylinder.

The mass flow rate out is

(5.23)#\[\begin{equation} \dot m_{\rm out} = \rho \dot V = \rho \frac{\pi D_2^2}{4} \sqrt{2gh} \end{equation}\]

where \(\dot V\) is the volumetric flow rate out of the hole, which we compute from the cross-sectional area of the hole (a circle with diameter \(D_2\) = 0.01 m) and the model for the velocity leaving it.

Inserting both into the unsteady balance, applying rules of differentiation, and simplifying gives

(5.24)#\[\begin{align} \dd{}{}{t}\left(\rho \frac{\pi D_1^2}{4} h\right) &= -\rho \frac{\pi D_2^2}{4} \sqrt{2gh} \\ \rho \frac{\pi D_1^2}{4} \dd{}{h}{t} &= -\rho \frac{\pi D_2^2}{4} \sqrt{2gh} \\ \frac{dh}{dt} &= -\left(\frac{D_2}{D_1}\right)^2 \sqrt{2gh} \end{align}\]

This is a separable differential equation

(5.25)#\[\begin{align} \int \frac{1}{\sqrt{h}} \d{h} &= \int -\left(\frac{D_2}{D_1}\right)^2 \sqrt{2g} \d{t} \\ 2\sqrt{h} &= -t \left(\frac{D_2}{D_1}\right)^2 \sqrt{2g} + c \end{align}\]

Find the integration constant c using the initial condition

(5.26)#\[\begin{equation} 2 \sqrt{2} = c \end{equation}\]

The tank drains when \(h = 0\), so substitute this, c, and numerical values:

(5.27)#\[\begin{align} 0 &= -t \left(\frac{0.01}{1}\right)^2 \sqrt{2 \cdot 9.8} + 2 \sqrt{2} \\ t &= 2 \left(\frac{1}{0.01}\right)^2 \sqrt{\frac{2}{2 \cdot 9.8}} = 6400 \end{align}\]

This time is in seconds because all units are SI, so the tank drains in about 1.8 hours.

5.2.1. Skill builder problems#

Solve the following:

  1. \(y'+(x+2)y^2 = 0, \quad y(1) = 1\)

    Solution

    Separate and integrate:

    (5.28)#\[\begin{align} \dd{}{y}{x} &= -(x+2)y^2 \\ \int\frac{\d{y}}{y^2} &= -\int (x+2) \d{x} \\ -\frac{1}{y} &= -\left(\frac{x^2}{2} + 2x\right) + c \end{align}\]

    Apply initial condition \(y(1) = 1\):

    (5.29)#\[\begin{equation} -1 = -\left(\frac{1}{2} + 2 \right) + c \end{equation}\]

    so \(c = 3/2\). Hence,

    (5.30)#\[\begin{equation} y = \frac{2}{x^2+4x-3} \end{equation}\]

  2. \(yy'+4x = 0, \quad y(0) = 3\)

    Solution

    Separate and integrate:

    (5.31)#\[\begin{align} y \frac{dy}{dx} &= -4x \\ \int y \d{y} &= \int-4x \d{x} \\ -\frac{y^2}{2} &= -2x^2 + c \\ \end{align}\]

    Apply initial condition \(y(0) = 3\):

    (5.32)#\[\begin{equation} -\frac{9}{2} = c \end{equation}\]

    so

    (5.33)#\[\begin{align} y^2 &= 9-4x^2 \\ y &= \pm \sqrt{9-4x^2} \end{align}\]

    The negative root does not satisfy the initial condition, so choose the positive root:

    (5.34)#\[\begin{equation} y = \sqrt{9-4x^2} \end{equation}\]

  3. \(\displaystyle y' = \frac{x-1}{y}e^{-y^2}, \quad y(0) = 1\)

    Solution

    Separate and integrate:

    (5.35)#\[\begin{align} \int y e^{y^2} \d{y} &= \int (x-1) \d{x} \\ \frac{1}{2} e^{y^2} &= \frac{x^2}{2} - x + c \end{align}\]

    Apply initial condition \(y(0) = 1\):

    (5.36)#\[\begin{equation} \frac{1}{2} e = c \end{equation}\]

    Hence,

    (5.37)#\[\begin{align} e^{y^2} &= x^2 - 2x + e \\ y^2 &= \ln(x^2 - 2x + e) \\ y &= \pm \sqrt{\ln(x^2 - 2x + e)} \end{align}\]

    The negative root again does not meet the initial condition, so choose the positive one:

    (5.38)#\[\begin{equation} y = \sqrt{\ln(x^2 - 2x + e)} \end{equation}\]
Contents