Integrating factor

5.5. Integrating factor#

What do we do when an ODE is not exact? For example,

(5.102)#\[\begin{equation} -y \d{x} + x \d{y} = 0 \end{equation}\]

has

(5.103)#\[\begin{align} P &= -y & Q &= x \\ \pp{}{P}{y} &= -1 & \pp{}{Q}{x} &= 1 \end{align}\]

so it is not exact. However, we may be able to make it exact if we multiply by an integrating factor. For example, let’s try a factor \(F = 1/x^2\). Multiplying through by F:

(5.104)#\[\begin{align} -\frac{y}{x^2} \d{x} + \frac{1}{x} \d{y} = 0 \end{align}\]

so

(5.105)#\[\begin{align} P &= -\frac{y}{x^2} & Q &= \frac{1}{x} \\ \pp{}{P}{y} &= -\frac{1}{x^2} & \pp{}{Q}{x} &= -\frac{1}{x}^2 \end{align}\]

Now the ODE is exact and can be solved using techniques we learned previously.

5.5.1. Finding the integrating factor#

Let’s use these formulas to arrive at the integrating factor we used above:

(5.111)#\[\begin{equation} R = \frac{1}{x}(-1 - 1) = -\frac{2}{x} \end{equation}\]

is a function of only x so

(5.112)#\[\begin{align} F(x) &= \exp\left( \int -\frac{2}{x} \d{x} \right) \\ &= \exp\left( -2 \ln x\right) \\ &= \left( e^{\ln x} \right)^{-2} \\ &= \frac{1}{x^2} \end{align}\]

Note that this is not the only suitable integrating factor! Let’s try the S route for fun:

(5.113)#\[\begin{equation} S = -\frac{Q}{P} R = -\frac{x}{-y} \left( -\frac{2}{x}\right) = -\frac{2}{y} \end{equation}\]

S is a function of only y so

(5.114)#\[\begin{equation} F = \exp\left( \int -\frac{2}{y} \d{y} \right) = \frac{1}{y^2} \end{equation}\]

is another suitable integrating factor.

5.5.2. Application to linear first-order ODEs#

Example: Mole balance on a tank with increasing inlet/outlet flow rate.

A stream with concentration \(c_{{\rm f},{\rm A}}\) of solute A flows into a tank with initial volume V at a continuously increasing volumetric flow rate \(Q = \dot q t\), where \(\dot q\) is the rate of increase in the flow rate and t is time. A well-mixed stream is withdrawn from the tank at the same rate.

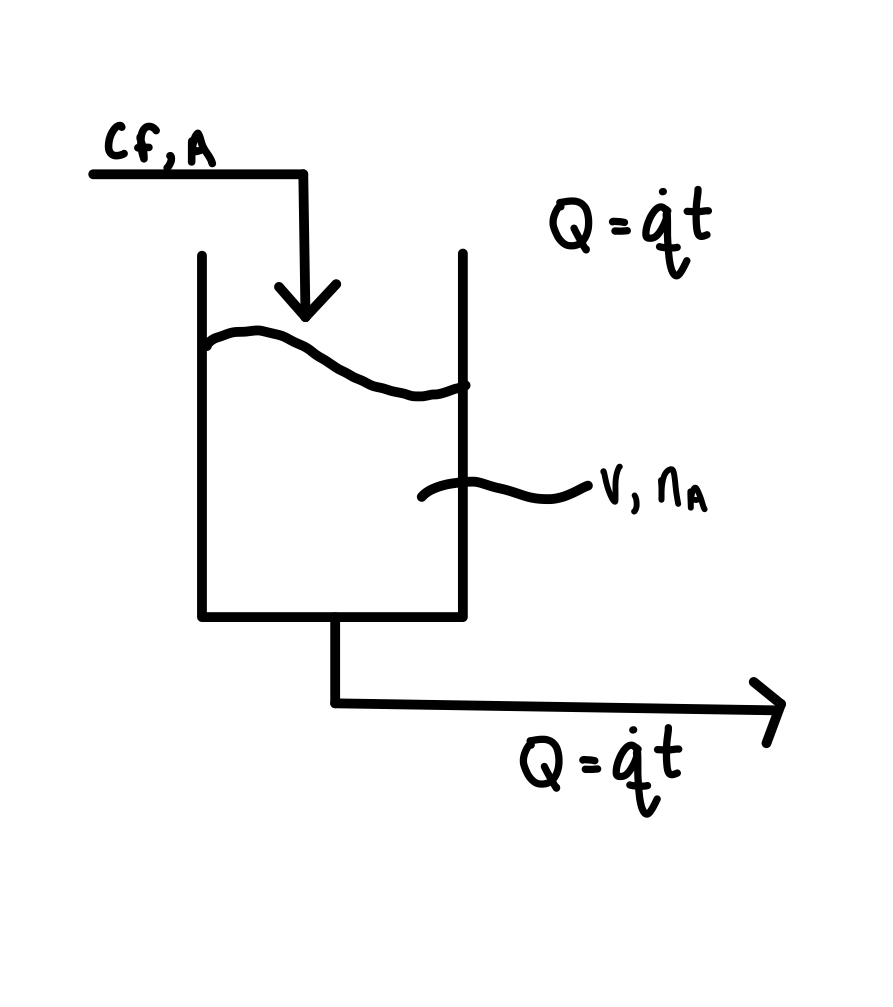
Tank with inlet and outlet flows and varying concentrations

If there are initial \(n_{{\rm A},0}\) moles of the solute, derive an expression for the number of moles in the tank \(n_{\rm A}\) as a function of time.

Formulate overall mole balances based on entering and exit streams.

\[ \dd{}{n_{\rm A}}{t} = \dot{n}_{{\rm A},\rm{in}} - \dot{n}_{{\rm A},\rm{out}} \]

Replace the molar flowrates with the equivalent concentrations and volumetric flow rates

(5.117)#\[\begin{align} \dot{n}_{{\rm A},\rm{in}} &= c_{{\rm f},{\rm A}} Q = c_{{\rm f},{\rm A}} \dot{q}t \\ \dot{n}_{{\rm A},\rm{out}} &= \frac{n_{\rm A}}{V} Q = \frac{n_{\rm A}}{V} \dot{q} \end{align}\]

so the initial value problem is

(5.118)#\[\begin{equation} \dot{n}_{\rm A} = c_{{\rm f},{\rm A}}\dot{q}t - \frac{n_{\rm A}}{V} \dot{q}t, \quad n_{\rm A}(0) = n_{{\rm A},0} \end{equation}\]

Rewrite in standard form

(5.119)#\[\begin{equation} \dot{n}_{A} + \left(\frac{\dot{q}t}{V}\right) n_{\rm A} = c_{{\rm f},{\rm A}} \dot{q}t \end{equation}\]

This is a linear first-order ODE with

(5.120)#\[\begin{equation} p = \frac{\dot{q}t}{V} \qquad r = c_{{\rm f},{\rm A}} \dot{q}t \end{equation}\]

that can be solved using an integrating factor:

(5.121)#\[\begin{equation} F = e^{\int p \d{t}} = \exp\left(\int{\frac{\dot{q}t}{V} \d{t}}\right) = \exp\left(\frac{1}{2}\frac{\dot{q} t^2}{V}\right) \end{equation}\]

Then, evaluate the integral

(5.122)#\[\begin{align} \int F r \d{t} &= \int \exp\left(\frac{1}{2}\frac{\dot{q} t^2}{V}\right) c_{{\rm f},{\rm A}}\dot{q}t \d{t} \\ &= \int{e^{u}c_{{\rm f},{\rm A}}Vdu} \\ &= c_{{\rm f},{\rm A}}V e^u \\ &= c_{{\rm f},{\rm A}}V \exp\left(\frac{1}{2}\frac{\dot{q}t^2}{V}\right) \end{align}\]

using the u substitution:

(5.123)#\[\begin{align} u &= \frac{1}{2}\frac{\dot{q} t^2}{V} \\ \d{u} &= \frac{\dot{q} t}{V} \d{t} \end{align}\]

Last, combine the results:

(5.124)#\[\begin{align} n_{\rm A}(t) &= \frac{1}{F} \left(\int F r \d{t} + c \right) \\ &= c_{{\rm f},{\rm A}} V + c \exp\left(-\frac{1}{2}\frac{\dot{q}t^2}{V}\right) \end{align}\]

Use the inital conditions to evaluate the integration constant:

(5.125)#\[\begin{align} n_{\rm A}(0) &= c_{{\rm f},{\rm A}}V + c = n_{{\rm A},0} \\ c &= n_{{\rm A}, 0} - c_{{\rm f},{\rm A}} V \end{align}\]

The final result is:

(5.126)#\[\begin{equation} n_{\rm A}(t) = c_{{\rm f},{\rm A}}V + (n_{{\rm A},0} - c_{{\rm f},{\rm A}}V) \exp\left(-\frac{1}{2}\frac{\dot{q}t^2}{V}\right) \end{equation}\]

Example: Hormone level (again)

We had

(5.127)#\[\begin{equation} c' + kc = A + B\cos\left(\frac{\pi t}{12}\right), \quad c(0) = c_0 \end{equation}\]

This is a linear first-order ODE with:

(5.128)#\[\begin{equation} p = kc \qquad r = A + B\cos\left(\frac{\pi t}{12}\right) \end{equation}\]

that can be solved using an integrating factor:

(5.129)#\[\begin{equation} F = e^{\int k \d{t}} = e^{kt} \end{equation}\]

Then, evaluate the integral using the table of integrals or integration by parts to evaluate the second integral in the equation

(5.130)#\[\begin{align} \int F r \d{t} &= \int e^{kt} \left[A+B\cos\left(\frac{\pi t}{12}\right)\right]\d{t} \\ &= A\int e^{kt} \d{t} + B \int e^{kt} \cos\left(\frac{\pi t}{12}\right)\d{t} \\ &= \frac{A}{k} e^{kt} + B \frac{e^{kt}}{k^{2}+(\pi/12)^2} \Biggl[k \cos{(\frac{\pi t}{12})} + \frac{\pi}{12}\sin{\left(\frac{\pi t}{12}\right)}\Biggr] \end{align}\]

The general solution is:

(5.131)#\[\begin{align} c(t) &= \frac{1}{F} \left(\int F r \d{t} + c^* \right) \\ &= \frac{A}{k} + \frac{B}{k^{2}+(\pi/12)^2} \Biggl[k \cos\left(\frac{\pi t}{12}\right) + \frac{\pi}{12}\sin{\left(\frac{\pi t}{12}\right)}\Biggr] + c^* e^{-kt} \end{align}\]

Use the inital condition to evaluate the integration constant:

(5.132)#\[\begin{align} c(0) &= \frac{A}{k} + \frac{B}{k^{2}+(\pi/12)^2} k + c^* = c_0 \\ c^* &= c_0 - \frac{A}{k} - \frac{B}{k^{2}+(\pi/12)^2} k \end{align}\]

The final solution is:

(5.133)#\[\begin{align} c(t) &= \frac{A}{k} + \frac{B}{k^{2}+(\pi/12)^2} \Biggl[k \cos\left(\frac{\pi t}{12}\right) + \frac{\pi}{12}\sin{\left(\frac{\pi t}{12}\right)}\Biggr] \\ &+ \Biggl[c_0 - \frac{A}{k} - \frac{Bk}{k^{2}+(\pi/12)^2} \Biggr] e^{-kt} \end{align}\]

5.5.3. Skill builder problems#

Solve the following differential equations:

  1. \(\displaystyle y' = \frac{x^4 + y^2}{xy}\)

    Solution

    This ODE is not in the standard form, so we need to first rearrange:

    (5.134)#\[\begin{align} xy \d{y} = (x^4+y^2) \d{x} \\ (x^4 + y^2) \d{x} - xy \d{y} = 0 \end{align}\]

    so:

    (5.135)#\[\begin{align} P &= x^4 + y^2 \\ Q &= -xy \end{align}\]

    Check to see if the ODE is exact:

    (5.136)#\[\begin{align} \td{}{P}{y}{x} &= 2y \\ \td{}{Q}{x}{y} &= -y \end{align}\]

    The two partial derivatives are not equal, so the ODE is not exact. In order to make it exact, we need to find an integrating factor F. First, compute:

    (5.137)#\[\begin{align} R &= \frac{1}{Q}\left[\td{}{P}{y}{x} - \td{}{Q}{x}{y} \right] \\ &=\frac{1}{-xy}(2y-(-y)) \\ &= -\frac{3}{x} \end{align}\]

    R is a function of only x, so use it to compute F

    (5.138)#\[\begin{equation} F = \exp\left(\int \frac{-3}{x} \d{x}\right) = e^{-3\ln(x)} = x^{-3} \end{equation}\]

    Apply the integrating factor to the original ODE:

    (5.139)#\[\begin{align} x^{-3}(x^4+y^2) \d{x} - x^{-3}(xy) \d{y} &= 0 \\ \left(x+\frac{y^2}{x^{-3}}\right) \d{x} - \frac{y}{x^2} \d{y} &= 0 \end{align}\]

    Integrate the Q of our exact ODE with respect to y:

    (5.140)#\[\begin{equation} f(x,y) = \int -\frac{y}{x^2} \d{y} = \frac{-y^2}{2x^2}+k(x) \end{equation}\]

    where k is an unknown function of x. Then, differentiate f with respect to x and compare to P of the exact ODE:

    (5.141)#\[\begin{align} \td{}{f}{x}{y} = \frac{y^2}{x^3} + k'(x) &= P = x + \frac{y^2}{x^3} \\ k'(x) &= x \\ \end{align}\]

    This ODE for k can be integrated directly (neglecting the integration constant)

    (5.142)#\[\begin{equation} k = \int x \d{x} = \frac{x^2}{2} \end{equation}\]

    Putting it all together,

    (5.143)#\[\begin{align} f = \frac{-y^2}{2x^2} + \frac{x^2}{2} = c \end{align}\]

    is an implicit solution of the ODE.

  2. \(\displaystyle y' = -\frac{e^{x+y} + ye^y}{x e^y - 1}\)

    Solution

    This ODE is not in the standard form, so we need to first rearrange:

    (5.144)#\[\begin{align} (e^{x+y} + ye^y) \d{x} + (x e^y - 1) \d{y} = 0 \end{align}\]

    so

    (5.145)#\[\begin{align} P &= e^{x+y} + ye^y \\ Q &= x e^y - 1 \end{align}\]

    Check if the differential equation is exact:

    (5.146)#\[\begin{align} \td{}{P}{y}{x} &= e^{x+y} + y e^y + e^y \\ \td{}{Q}{x}{y} &= e^y \end{align}\]

    These are not equal, so the equation is not exact. To make it exact, find integrating factor F. The R formula gives:

    (5.147)#\[\begin{align} R &= \frac{1}{Q}\left[\td{}{P}{y}{x} - \td{}{Q}{x}{y} \right] \\ &=\frac{1}{x e^y - 1}(e^{x+y} + y e^y + e^y - e^y) \\ &= \frac{e^y(e^x + y)}{x e^y - 1} \end{align}\]

    this is not a function of only x, so try the S formula:

    (5.148)#\[\begin{align} S &= -\frac{Q}{P} R \\ &= -\frac{e^y(e^x + y)}{e^{x+y} + y e^y} \\ &= -1 \end{align}\]

    This is a function of, at most, y so:

    (5.149)#\[\begin{equation} F = \exp\left(\int S\d{y} \right) = e^{-y} \end{equation}\]

    Multiply the equation by F:

    (5.150)#\[\begin{equation} (e^x + y) \d{x} + (x - e^{-y}) \d{y} = 0 \end{equation}\]

    Now the equation is exact so integrate the new P with respect to x:

    (5.151)#\[\begin{equation} f(x,y) = \int (e^x + y) \d{x} = e^x + xy + k(y) \end{equation}\]

    where k is an unknown function of y. Then, differentiate f with respect to y and compare to Q:

    (5.152)#\[\begin{align} \td{}{f}{x}{y} = x + k'(y) &= Q = x - e^{-y} \\ k' &= -e^{-y} \end{align}\]

    This ODE for k can be integrated directly (neglecting the integration constant)

    (5.153)#\[\begin{align} k(y) = \int -e^{-y} \d{y} = e^{-y} \end{align}\]

    Putting it all together,

    (5.154)#\[\begin{align} f(x, y) = e^x + e^{-y} + xy = c \end{align}\]

    is an implicit solution for the ODE.

  3. \(\displaystyle y' = y + 1 - 2x\)

    Solution

    Rewrite in linear form:

    (5.155)#\[\begin{align} y' - y = 1 - 2x \end{align}\]

    where

    (5.156)#\[\begin{align} p = -1 \qquad r = 1 - 2x \end{align}\]

    Find integrating factor:

    (5.157)#\[\begin{align} F = e^{\int p\d{x}} = e^{\int -1 \d{x}} = e^{-x} \end{align}\]

    Then, evaluate the integral

    (5.158)#\[\begin{equation} \int F r \d{x} = \int e^{-x} (1-2x) \d{x} \end{equation}\]

    This integral can be evaluated by parts using the tabular method:

    sign

    \(u\)

    \(\d{v}\)

    \(e^{-x}\)

    \(+\)

    \(1-2x\)

    \(-e^{-x}\)

    \(-\)

    \(-2\)

    \(e^{-x}\)

    \(0\)

    so

    (5.159)#\[\begin{equation} \int F r \d{x} = (2x-1)e^{-x} + 2 e^{-x} = (2x + 1) e^{-x} \end{equation}\]

    Putting it all together:

    (5.160)#\[\begin{align} y &= \frac{1}{F}\left(\int F r \d{x} + c \right) \\ &= e^x \left[ (2x + 1) e^{-x} + c \right] \\ &= 1 + 2x + c e^x \end{align}\]
Contents