Definition

5.1. Definition#

An ordinary differential equation (ODE) contains one or more derivatives of an unknown function of one variable.

(5.1)#\[\begin{align} &y' = \cos x \\ &y'' + 9y = 0 \\ &x^2 y''' y' + 2e^x y^4 = (x^2 + 2)y^2 \end{align}\]

The order of an ODE is its highest derivative. First-order ODEs in explicit form look like:

(5.2)#\[\begin{equation} F(x, y, y') = 0 \end{equation}\]

and in implicit form look like:

(5.3)#\[\begin{equation} y' = f(x, y) \end{equation}\]

When do we see first-order ODEs in chemical engineering?

  • Unsteady mass/energy balances

  • Chemical kinetics

5.1.1. Direction fields and initial value problems#

ODEs have families of solutions due to integration constants. The direction field (or slope field) is obtained by plotting the slope at (x, y) from \(y' = f(x, y)\), and it shows how a point will evolve.

Example: Direction field

Given the first-order ODE

(5.4)#\[\begin{equation} y' = xy \quad y(0) = 1 \end{equation}\]

Draw the slope field, then verify that

(5.5)#\[\begin{equation} y = c e^{x^2 / 2} \end{equation}\]

is a general solution.

The direction field is

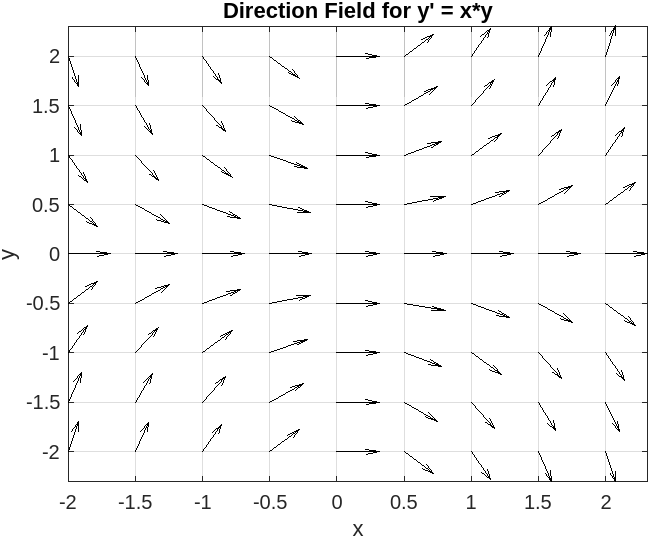
Directional field diagram

Now, let’s verify the proposed solution. The first derivative of y is

(5.6)#\[\begin{equation} y' = c x e^{x^2/2} \end{equation}\]

Substituting y and \(y'\) in the differential equation

(5.7)#\[\begin{align} y' &= x y \\ c x e^{x^2 / 2} &= x (c e^{x^2 / 2}) \end{align}\]

shows this is indeed a solution.

To obtain a specific solution, an initial condition specifying a point \(y(x_0) = y_0\) is needed. A first-order ODE with an initial condition is called an initial value problem.

Example: Applying initial condition

For the first-order ODE above, find the solution when \(y(0) = 1\).

Substitute \(x = 0\) and \(y = 1\) into the general solution \(y = c e^{-x^2/2}\) to determine \(c\):

(5.8)#\[\begin{equation} 1 = y(0) = c e^0 = c \end{equation}\]

This gives the solution

(5.9)#\[\begin{equation} y = e^{x^2/2} \end{equation}\]
Contents