6.1. Definition

Many dynamic processes can occur simultaneously, giving more than one ODE. For example, consider two tanks. Tank 1 has concentration \(c_1\) of a solute and Tank 2 has concentration \(c_2\). Tank 1 flows into Tank 2, which is then passed through a pump and recycled back to Tank 1.

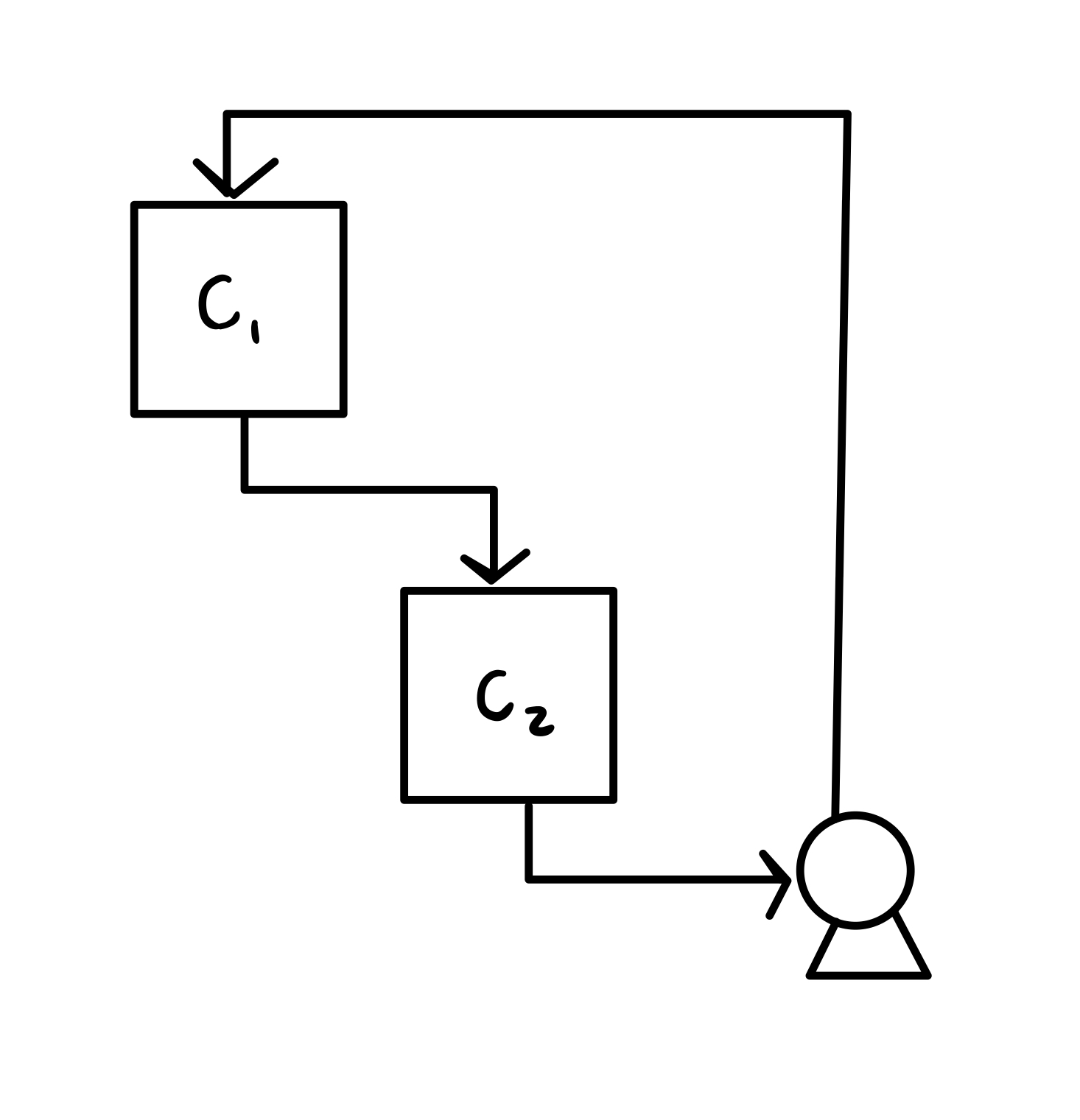
Eventually, the two concentrations should equalize, but how do they evolve to over time? \(c_1\) and \(c_2\) can be modeled using unsteady mass balances. This is a system of first-order ODEs that can be solved simultaneously.

The general, explicit form of a system of first-order ODEs is:

(6.1)\[\begin{align} y_1' &= f_1(t, y_1, \cdots, y_n)\\ \vdots \\ y_n' &= f_n(t, y_1, \cdots, y_n) \end{align}\]

where t is the independent variable, \((y_1, \cdots, y_n)\) are the n dependent variables, and \((f_1, \cdots, f_n)\) are the n right-hand side functions of the n ODEs. We will notate this system more compactly using vectors

(6.2)\[\begin{equation} \vv{y}' = \vv{f}(t, \vv{y}) \end{equation}\]

where y is the column vector of dependent variables, f is the column vector of right-hand side functions, and \(\vv{y}'\) is a shorthand for the column vector of first derivatives of all dependent variables.

6.1.1. Successive substitution

Some systems of first-order ODEs have a special structure that allows you to solve one equation at a time, then substitute into another that can now be solved. This process can be repeated successively to solve for all dependent variables.

Example: Reaction network

We are analyzing a simple reaction sequence occuring in a batch reactor:

(6.3)\[\begin{equation} {\rm A} \xrightarrow{k_1} {\rm B} \xrightarrow{k_2} {\rm C} \end{equation}\]

where \(k_1\) and \(k_2\) are reaction rate constants. At \(t = 0\), only species A is present at concentration \(c_{{\rm A},0}\). Determine the concentration of B as a function of time. What happens in the special case \(k_1 = k_2\)?

---

Unsteady mole balances give

(6.4)\[\begin{align} \dd{}{c_{\rm A}}{t} &= -k_1 c_{\rm A} \\ \dd{}{c_{\rm B}}{t} &= k_1 c_{\rm A} - k_2 c_{\rm B} \\ \dd{}{c_{\rm C}}{t} &= k_2 c_{\rm B} \end{align}\]

These ODES can be solved by first finding \(c_{\rm A}\), then \(c_{\rm B}\), and last \(c_{\rm C}\)! The ODE for \(c_{\rm A}\) is separable:

(6.5)\[\begin{align} \int \frac{\d{c_{\rm A}}}{c_{\rm A}} &= \int -k_1 \d{t} \\ \ln c_{\rm A} &= -k_1 t + K \end{align}\]

Applying the initial condition \(c_{\rm A}(0) = c_{{\rm A},0}\) gives:

(6.6)\[\begin{equation} c_{\rm A} = c_{{\rm A}, 0} e^{-k_1 t} \end{equation}\]

Next, use the solution for \(c_{\rm A}\) to solve \(c_{\rm B}\):

(6.7)\[\begin{align} \dd{}{c_{\rm B}}{t} &= k_1 c_{\rm A,0}e^{-k_1 t} -k_2 c_{\rm B} \\ \dd{}{c_{\rm B}}{t} &+ k_2 c_{\rm B} = k_1 c_{\rm A,0}e^{-k_1 t} \end{align}\]

This is a linear first-order ODE with

(6.8)\[\begin{equation} p = k_2 \qquad r =k_1 c_{\rm A,0}e^{-k_1 t} \end{equation}\]

that can be solved using an integrating factor:

(6.9)\[\begin{align} F &= e^{\int k_2 \d{t}} = e^{k_2 t} \\ \int F r \d{t} &= \int e^{k_2 t} k_1 c_{\rm A,0} e^{-k_1 t} \d{t} \\ &= k_1 c_{\rm A,0} \int e^{(k_2 -k_1)t} \d{t} \\ &= c_{\rm A,0} \frac{k_1}{k_2 -k_1} e^{(k_2 -k_1)t} \end{align}\]

Hence,

(6.10)\[\begin{align} c_{\rm B} &= \frac{1}{F}\left(\int Fr\d{t} + K \right) \\ &= c_{\rm A,0} \frac{k_1}{k_2 - k_1} e^{-k_1 t} + K e^{-k_2 t} \end{align}\]

Applying the initial condition

(6.11)\[\begin{align} c_{\rm B}(0) &= c_{\rm A,0} \frac{k_1}{k_2 - k_1} + K = 0 \\ K &= -c_{\rm A,0} \frac{k_1}{k_2 - k_1} \end{align}\]

Hence,

(6.12)\[\begin{equation} c_{\rm B} =c _{\rm A,0} \frac{k_1}{k_2 -k_1} \left(e^{-k_1 t} - e^{-k_2 t} \right) \end{equation}\]

If \(k_1 = k_2\), the solution appears to have an issue because there is a “divide by zero”. However, we can actually evaluate this behavior as a limit! Let’s set \(k_1 = k\), and take the limit as \(k_2 \to k\):

(6.13)\[\begin{align} \lim_{k_2 \to k} c_{\rm B} &= c_{{\rm A},0} k \lim_{k_2 \to k} \frac{e^{-k t} - e^{-k_2 t}}{k_2 -k_1} \\ &= c_{{\rm A},0} k \lim_{k_2 \to k} \frac{t e^{-k_2 t}}{1} \\ &= c_{{\rm A},0} k t e^{-k t} \end{align}\]

where in the second line, we made use of L’Hopital’s rule to evaluate the limit.

6.1.2. Skill builder problems

1. Solve the IVP

   (6.14)\[\begin{align} y_1' &= 1-2y_1, & y_1(0) &= 0\\ y_2' &= 2y_1 - y_1y_2, & y_2(0) &= 0 \end{align}\]
   Solution

   We begin by solving for \(y_1\) in terms of x. The ODE is separable and therefore can be solved using separation of variables.

   (6.15)\[\begin{align} \int \frac{dy_1}{1-2y_1} &= \int dx \\ -\frac{1}{2} \ln{\left(1-2y_1\right)} &= x + c_0 \\ \ln{\left(1-2y_1\right)} &= -2x + c_1 \\ 1 - 2y_1 &= c_2 e^{-2x} \\ y_1 &= \frac{1}{2} \left(1- c_2 e^{-2x}\right) \\ \end{align}\]

   Now, use the initial condition \(y_1(0)= 0\) to solve for \(c_2\):

   (6.16)\[\begin{equation} y_1(0) = \frac{1}{2}\left(1-c_2\right) = 0 \end{equation}\]

   so \(c_2 = 1\) and

   (6.17)\[\begin{equation} y_1 = \frac{1}{2} \left(1-e^{-2x}\right) \end{equation}\]

   Now, we can solve for \(y_2\) knowing \(y_1\) and recognizing that \(y_2\) can also be solved via separation of variables

   (6.18)\[\begin{align} y_2' &= y_1\left(2-y_2\right) \\ \int \frac{dy_2}{2-y_2} &= \int \frac{1}{2}\left(1-e^{-2x}\right) \d{x} \\ -\ln{\left(2-y_2\right)} &= \frac{1}{2}\left(x + \frac{1}{2}e^{-2x}\right) + c_0\\ 2 - y_2 &= c_1 \exp\left[-\frac{1}{2}\left(x+ \frac{1}{2}e^{-2x}\right)\right] \\ y_2 &= 2 - c_1 \exp\left[-\frac{1}{2}\left(x+\frac{1}{2}e^{-2x}\right)\right] \\ \end{align}\]

   Again, use the initial condition \(y_2(0)= 0\) to solve for \(c_1\):

   (6.19)\[\begin{align} y_2(0) &= 2 - c_1 e^{-1/4} = 0 \\ c_1 &= 2e^{1/4} \end{align}\]

   Therefore,

   (6.20)\[\begin{equation} y_2 = 2\left[1-\exp\left(\frac{1}{4}-\frac{x}{2}-\frac{1}{4}e^{-2x}\right)\right] \end{equation}\]