Homogeneous linear first-order ODEs with constant coefficients

6.3. Homogeneous linear first-order ODEs with constant coefficients#

Systems of homogeneous linear first-order ODEs with constant coefficients can be written in the form:

(6.23)#\[\begin{equation} \vv{y}' = \vv{A} \vv{y} \end{equation}\]

Let’s guess a solution of the form:

(6.24)#\[\begin{align} \vv{y} &= e^{\lambda t} \vv{x} \\ \vv{y}' &= \lambda e^{\lambda t} \vv{x} \end{align}\]

Substituting in the ODE:

(6.25)#\[\begin{align} \lambda e^{\lambda t} \vv{x} &= \vv{A} e^{\lambda t}\\ \lambda \vv{x} &= \vv{A} \vv{x} \end{align}\]

We find that our solution must satisfy an eigenvalue problem! \(\lambda\) is an eigenvalue and x is an eigenvector of A. We know an n x n matrix has n eigenvalues. Let’s suppose the corresponding eigenvectors are all linearly independent. What do we do?

In practice, this means that

(6.27)#\[\begin{equation} \vv{y} = \sum_{i=1}^n c_i e^{\lambda_i t} \vv{x}_i = c_1 e^{\lambda_1 t}\vv{x}_1 + \cdots + c_n e^{\lambda_n t}\vv{x}_n \end{equation}\]

(There are some cases this fails, but we will not cover them.) To apply the initial condition \(\vv{y}(0) = \vv{y}_0\), substitute and rewrite as a linear system:

(6.28)#\[\begin{align} \vv{y}(0) = c_1 \vv{x}_1 + \cdots c_n \vv{x}_n &= \vv{y}_0 \\ \vv{X} \vv{c} &= \vv{y}_0 \end{align}\]

where \(\vv{X} = [\vv{x}_1 \cdots \vv{x}_n]\) is the matrix whose columns are the eigenvectors of A and c is the column vector of unknown coefficients.

Example: Reaction network (again)

We previously analyzed the concentration of three species (A, B, and C) undergoing a sequence of first-order reactions, \(A \to B \to C\), where the first reaction has rate constant \(k_1\) and the second reaction has rate constant \(k_2\). It gave rise to a system of first-order ODEs:

(6.29)#\[\begin{equation} \vv{c}' = \vv{A} \vv{c}, \quad \vv{c}(0) = \begin{bmatrix} c_{{\rm A},0} \\ 0 \\ 0 \end{bmatrix} \end{equation}\]

where

(6.30)#\[\begin{equation} \vv{c} = \begin{bmatrix} c_{\rm A} \\ c_{\rm B} \\ c_{\rm C} \end{bmatrix} \qquad \vv{A} = \begin{bmatrix} -k_1 & 0 & 0 \\ k_1 & -k_2 & 0 \\ 0 & k_2 & 0 \end{bmatrix} \end{equation}\]

Solve again using eigenvalues and eigenvectors.

A is lower triangular, so its eigenvalues are: \(\lambda_1 = -k_1\) \(\lambda_2 = -k_2\), and \(\lambda_3 = 0\). We need to find the corresponding eigenvectors. Starting with \(\lambda_1 = -k_1\):

(6.31)#\[\begin{equation} \vv{A} - \lambda_1 \vv{I} = \begin{bmatrix} 0 & 0 & 0 \\ k_1 & -k_2 + k_1 & 0 \\ 0 & k_2 & k_1 \end{bmatrix} \end{equation}\]

from which we obtain two equations:

(6.32)#\[\begin{align} k_1 x_1 - (k_2 - k_1) x_2 &= 0 \\ k_2 x_2 + k_1 x_3 &= 0 \\ \end{align}\]

with \(x_3\) free. Taking \(x_3 = 1\) gives

(6.33)#\[\begin{equation} \vv{x}_1 = \begin{bmatrix} \dfrac{-k_2 - k_1}{k_2} \\ \dfrac{-k_1}{k_2} \\ 1 \end{bmatrix} \end{equation}\]

Next, we will solve with \(\lambda_2 = -k_2\), which gives:

(6.34)#\[\begin{equation} \vv{A} - \lambda_2 \vv{I} = \begin{bmatrix} k_2-k_1 & 0 & 0 \\ k_1 & 0 & 0 \\ 0 & k_2 & k_2 \end{bmatrix} \end{equation}\]

from which we obtain:

(6.35)#\[\begin{equation} \vv{x}_2 = \begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} \end{equation}\]

Finally, we solve with \(\lambda_3 = 0\), which gives:

(6.36)#\[\begin{equation} \vv{A} - \lambda_3 \vv{I} = \begin{bmatrix} -k_1 & 0 & 0 \\ k_1 & -k_2 & 0 \\ 0 & k_2 & 0 \end{bmatrix} \end{equation}\]

from which we obtain:

(6.37)#\[\begin{equation} \vv{x}_3 = \begin{bmatrix} 0\\ 0 \\ 1 \end{bmatrix} \end{equation}\]

Hence, the general solution is

(6.38)#\[\begin{equation} \vv{c} = a_1 e^{-k_1t} \begin{bmatrix} \dfrac{-k_2 - k_1}{k_2} \\ \dfrac{-k_1}{k_2} \\ 1 \end{bmatrix} + a_2 e^{-k_2t} \begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} + a_3 e^{0 t} \begin{bmatrix} 0\\ 0 \\ 1 \end{bmatrix} \end{equation}\]

Now, we apply the initial condition:

(6.39)#\[\begin{align} \begin{bmatrix} \dfrac{-k_2 - k_1}{k_2} & 0 & 0 \\ \dfrac{-k_1}{k_2} & -1 & 0 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix} c_{{\rm A},0}\\ 0 \\ 0 \end{bmatrix} \end{align}\]

Thus,

(6.40)#\[\begin{align} a_1 &= -c_{{\rm A},0}\frac{k_2}{k_2-k_1} \\ a_2 &= -\frac{k_1}{k_2}a_1 = c_{{\rm A},0}\frac{k_1}{k_2-k_1} \\ a_3 &= -a_1 - a_2 = c_{{\rm A},0} \end{align}\]

Finally, substitute these constants into the general solution and add across the rows to obtain solutions for each concentration:

(6.41)#\[\begin{align} c_{\rm A}(t) &= a_1e^{-k_1t}\frac{-k_2-k_1}{k_2} = c_{{\rm A},0}e^{-k_1t} \\ c_{\rm B}(t) &= a_1e^{-k_1t}\frac{-k_1}{k_2} - a_2e^{-k_2t} \\ &= c_{{\rm A},0}\frac{k_1}{k_2 - k_1}(e^{-k_1t} - e^{-k_2t}) \\ c_{\rm C}(t) &= a_1e^{-k_1t} + a_2e^{-k_2t} + a_3 \\ &= c_{{\rm A},0}\Biggl(1 - \frac{k_2}{k_2 - k_1} e^{-k_1t} + \frac{k_1}{k_2 - k_1} e^{-k_2t}\Biggr) \end{align}\]

This matches our old answer!

Example: Diffusion cell

Consider a diffusion cell consisting of two compartments with solute concentrations \(c_1\) and \(c_2\) separated by a membrane.

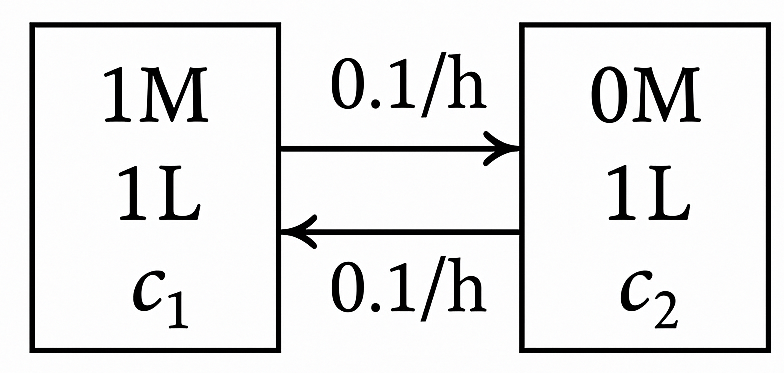
Diffusion cell

Based on unsteady mole balances, the concentrations change according to:

(6.42)#\[\begin{align} c_1' &= -0.1c_1 + 0.1c_2 \\ c_2' &= 0.1c_1 - 0.1c_2 \end{align}\]

Solve for \(c_1\) and \(c_2\) as a function of time if they are initially 1 M and 0 M, respectively.

Write in matrix form \(\vv{c}' = \vv{A} \vv{c}\), where

(6.43)#\[\begin{equation} \vv{c} = \begin{bmatrix}c_1 \\ c_2\end{bmatrix} \qquad \vv{A} = \begin{bmatrix} -0.1 & 0.1 \\ 0.1 & -0.1 \end{bmatrix} \end{equation}\]

Since A is symmetric, it has real eigenvalues:

(6.44)#\[\begin{align} |\vv{A} - \lambda \vv{I}| &= \begin{vmatrix} -0.1 - \lambda & 0.1 \\ 0.1 & -0.1 - \lambda \end{vmatrix}\\ &= (\lambda + 0.1)^2 - 0.1^2 \\ &= \lambda^2 + 0.2\lambda \\ & = \lambda(\lambda + 0.2) = 0 \end{align}\]

So, the eigenvalues are \(\lambda_1 = 0\) and \(\lambda_2 = -0.2\). Next, we find the eigenvectors:

(6.45)#\[\begin{align} \vv{A}-\lambda_1 \vv{I} &= \begin{bmatrix} -0.1 & 0.1 \\ 0.1 & -0.1 \end{bmatrix} \to \vv{x}_1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \\ \vv{A} - \lambda_2 \vv{I} &= \begin{bmatrix} 0.1 & 0.1 \\ 0.1 & 0.1 \end{bmatrix} \to \vv{x}_2 = \begin{bmatrix} 1 \\ -1 \end{bmatrix} \end{align}\]

The general solution is:

(6.46)#\[\begin{align} \vv{c}(t) &= a_1 e^{0t} \begin{bmatrix} 1 \\ 1 \end{bmatrix} + a_2 e^{-0.2t} \begin{bmatrix} 1 \\ -1 \end{bmatrix} \\ &= a_1 \begin{bmatrix} 1 \\ 1 \end{bmatrix} + a_2 e^{-0.2t} \begin{bmatrix} 1 \\ -1 \end{bmatrix} \end{align}\]

Apply the initial conditions by solving \(\vv{X}\vv{a} = \vv{c}(0)\) using Gauss-Jordan elimination:

(6.47)#\[\begin{align} \begin{bmatrix} 1 & 1 & 1\\ 1 & -1 & 0\end{bmatrix} \begin{matrix}\vphantom{R_1} \\ -R_1 \end{matrix} &\to \begin{bmatrix} 1 & 1 & 1\\ 0 & -2 & -1\end{bmatrix} \begin{matrix}\vphantom{R_1} \\ \div -2 \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 1\\ 0 & 1 & 1/2\end{bmatrix} \begin{matrix} -R_2 \\ \vphantom{R_2} \end{matrix} \\ &\to \begin{bmatrix} 1 & 0 & 1/2 \\ 0 & 1 & 1/2\end{bmatrix} \end{align}\]

so \(a_1 = a_2 = 1/2\). Substituting back, the general solution for \(\vv{c}(t)\) becomes:

(6.48)#\[\begin{equation} \vv{c}(t) = \frac{1}{2} \begin{bmatrix} 1 \\ 1 \end{bmatrix} + \frac{1}{2} e^{-0.2t} \begin{bmatrix} 1 \\ -1 \end{bmatrix} \end{equation}\]

or equivalently

(6.49)#\[\begin{align} c_1(t) &= \frac{1}{2} \left(1 + e^{-0.2 t}\right) \\ c_2(t) &= \frac{1}{2} \left(1 - e^{-0.2 t}\right) \end{align}\]

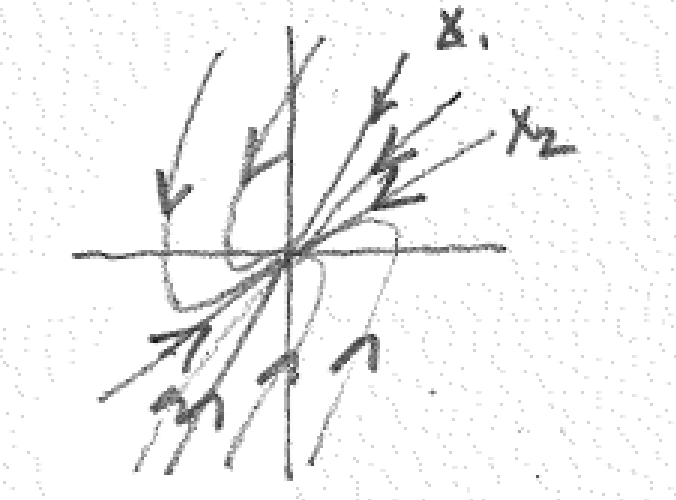
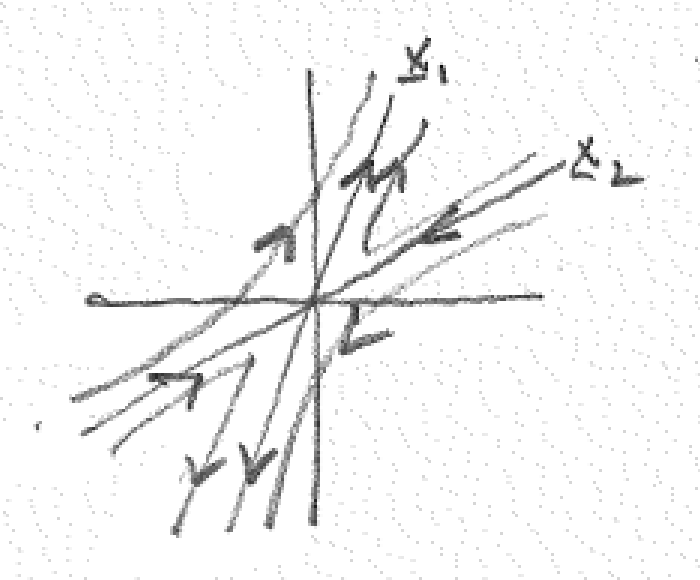
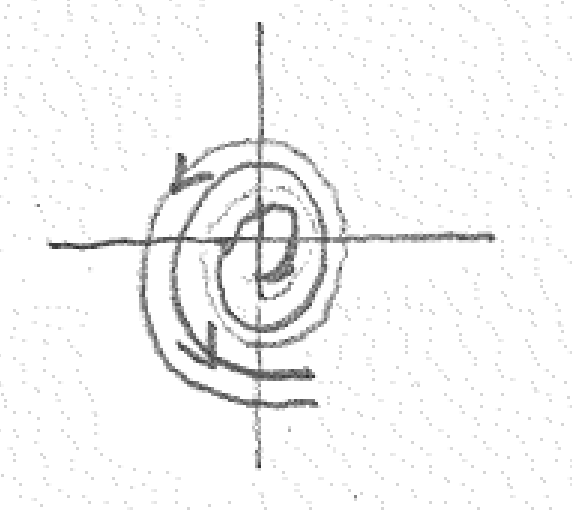
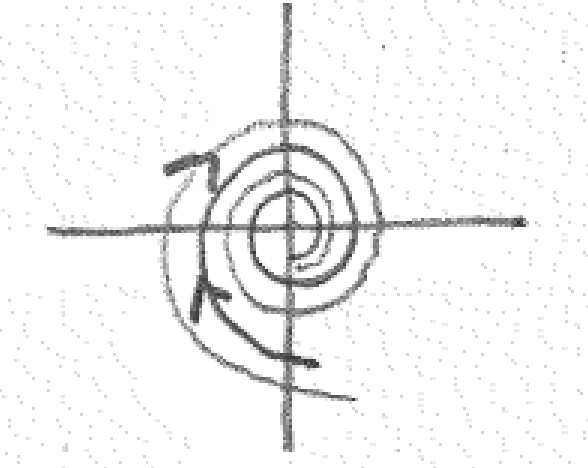
6.3.1. Types of critical points#

We can use the eigenvalues and eigenvectors to anticipate what solutions around critical points (\(\vv{y}' = \vv{0}\), or steady states) look like. We will focus our discussion on only 2 x 2 systems.

  • If the eigenvalues are real and distinct, \(\lambda_1 \ne \lambda_2\):

    Unstable improper node
    \[ \lambda_1 > \lambda_2 > 0 \]
    Unstable improper node
    Stable improper node
    \[ \lambda_1 < \lambda_2 < 0 \]
    Unstable improper node
    Saddle
    \[ \lambda_1 > 0, \quad \lambda_2 < 0 \]
    Saddle

  • If the eigenvalues are complex, \(\lambda_{1,2} = \alpha \pm i\omega\):

    Unstable spiral
    \[ \alpha > 0 \]
    Unstable spiral
    Stable spiral
    \[ \alpha < 0 \]
    Stable spiral
    Center
    \[ \alpha = 0 \]
    Center

    The direction of the orbit depends on the matrix and can be checked for some point. If

    (6.50)#\[\begin{equation} \vv{A} = \begin{bmatrix}a & b \\ c & d\end{bmatrix} \end{equation}\]

    The orbit is clockwise if \(b > c\) and counterclockwise if \(c < b\).

  • If the eigenvalues are real and repeated, \(\lambda_1 = \lambda_2\):

    Proper node / star

    A is a multiple of I.

    Proper node
    Degenerate node
    Degenerate node

6.3.2. Skill builder problems#

Solve the inital value problem \( \vv{y}' = \vv{A}\vv{y}\) with \(\vv{y}(0) = [1 \quad 0]^{\rm T}\) for the following matrices. Also classify the type of critical point using the eigenvalues.

  1. For:

    (6.51)#\[\begin{equation} \vv{A} = \begin{bmatrix} -2 & 0 \\ 0 & -2 \end{bmatrix} \end{equation}\]
    Solution

    A is upper triangular, so its eigenvalues are on its diagonal, \(\lambda_1 = \lambda_2 = -2\). Its eigenvectors are:

    (6.52)#\[\begin{equation} \vv{x}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \qquad \vv{x}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{equation}\]

    since \(\vv{A} - \lambda_{1,2} \vv{I} = 0\). The general solution is:

    (6.53)#\[\begin{equation} \vv{y} = c_1 e^{-2t} \begin{bmatrix} 1 \\ 0 \end{bmatrix} + c_2 e^{-2t} \begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{equation}\]

    To solve for the initial condition, form the augmented matrix for \(\vv{X}\vv{c} = \vv{y}(0)\),

    (6.54)#\[\begin{equation} \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} \end{equation}\]

    so \(c_1 = 1\) and \(c_2 = 0\).

    Hence,

    (6.55)#\[\begin{equation} \vv{y} =e ^{-2t} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{equation}\]

    or

    (6.56)#\[\begin{align} y_1 &= e^{-2t} \\ y_2 &= 0 \end{align}\]

    The critical point is a stable proper node because \(\lambda_{1} = \lambda_{2} < 0\) and A is a multiple of I.

  2. For:

    (6.57)#\[\begin{equation} \vv{A} = \begin{bmatrix} 0 & 3 \\ 12 & 0 \end{bmatrix} \end{equation}\]
    Solution

    First, find the eigenvalues of A:

    (6.58)#\[\begin{align} |\vv{A}-\lambda \vv{I}| &= \begin{vmatrix} -\lambda & 3 \\ 12 & -\lambda \end{vmatrix} \\ &= \lambda^{2}-36=0 \\ \lambda_{1,2} &= \pm 6 \end{align}\]

    For \(\lambda_1 = 6\),

    (6.59)#\[\begin{equation} \vv{A}-\lambda_1\vv{I} = \begin{bmatrix} -6 & 3 \\ 12 & -6 \end{bmatrix} \to \vv{x}_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix} \end{equation}\]

    For \(\lambda_2 = -6\),

    (6.60)#\[\begin{equation} \vv{A}-\lambda_2\vv{I} = \begin{bmatrix} 6 & 3 \\ 12 & 6 \end{bmatrix} \to \vv{x}_2 = \begin{bmatrix} 1 \\ -2 \end{bmatrix} \end{equation}\]

    The general solution is:

    (6.61)#\[\begin{equation} \vv{y} = c_1 e^{6t} \begin{bmatrix} 1 \\ 2 \end{bmatrix} + c_2 e^{-6t} \begin{bmatrix} 1 \\ -2 \end{bmatrix} \end{equation}\]

    To solve for the initial condition, form the augmented matrix for \(\vv{X}\vv{c} = \vv{y}(0)\),

    (6.62)#\[\begin{align} \begin{bmatrix} 1 & 2 & 1 \\ 2 & -2 & 0 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ -R_1 \end{matrix} & \to \begin{bmatrix} 1 & 1 & 1 \\ 0 & -4 & -2 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ \div -4 \end{matrix} \\ & \to \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & \frac{1}{2} \end{bmatrix} \begin{matrix} -R_2 \\ \vphantom{R_2} \end{matrix} \\ & \to \begin{bmatrix} 1 & 0 & \frac{1}{2} \\ 0 & 1 & \frac{1}{2} \end{bmatrix} \end{align}\]

    so \(c_1 = 1/2\) and \(c_2 = 1/2\) and

    (6.63)#\[\begin{equation} \vv{y} = \frac{1}{2}e^{-6t} \begin{bmatrix} 1 \\ 2 \end{bmatrix} + \frac{1}{2}e^{-6t} \begin{bmatrix} 1 \\ -2 \end{bmatrix} \end{equation}\]

    or

    (6.64)#\[\begin{align} y_1 & =\frac{1}{2}(e^{6t}+e^{-6t}) \\ y_2 &= e^{6t}+e^{-6t} \end{align}\]

    The critical point is a saddle because the eigenvalues are real and \(\lambda_1 > 0\) but \(\lambda_2 < 0\).

  3. For:

    (6.65)#\[\begin{equation} \vv{A} = \begin{bmatrix} 0 & 4 \\ -4 & 0 \end{bmatrix} \end{equation}\]
    Solution

    First, find the eigenvalues of A:

    (6.66)#\[\begin{align} |\vv{A} - \lambda \vv{I}| &= \begin{vmatrix} -\lambda & 4 \\ -4 & -\lambda \end{vmatrix} \\ &= \lambda^2 + 16 = 0 \\ \lambda_{1,2} &= \pm 4i \end{align}\]

    For \(\lambda_1 = 4i\),

    (6.67)#\[\begin{equation} \vv{A}-\lambda_1\vv{I} = \begin{bmatrix} -4i & 4 \\ -4 & -4i \end{bmatrix} \to \vv{x}_1 = \begin{bmatrix} -i \\ 1 \end{bmatrix} \end{equation}\]

    For \(\lambda_2 = -4i\),

    (6.68)#\[\begin{equation} \vv{A}-\lambda_2\vv{I} = \begin{bmatrix} 4i & 4 \\ -4 & 4i \end{bmatrix} \to \vv{x}_2 = \begin{bmatrix} i \\ 1 \end{bmatrix} \end{equation}\]

    The general solution is:

    (6.69)#\[\begin{equation} \vv{y} = c_1 e^{4it} \begin{bmatrix} -i \\ 1 \end{bmatrix} + c_2 e^{-4it} \begin{bmatrix} i \\ 1 \end{bmatrix} \end{equation}\]

    To solve for the initial condition, form the augmented matrix for \(\vv{X}\vv{c} = \vv{y}(0)\),

    (6.70)#\[\begin{align} \begin{bmatrix} -i & i & 1 \\ 1 & 1 & 0 \end{bmatrix} \begin{matrix} {\rm swap} \\ \vphantom{R_2}\end{matrix} &\to \begin{bmatrix} 1 & 1 & 0 \\ -i & i & 1 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ -R_1 \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 0 \\ 0 & 2i & 1 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ \div 2i \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & \frac{1}{2i} \end{bmatrix} \begin{matrix} -R_2 \\ \vphantom{R_2} \end{matrix} \\ &\to \begin{bmatrix} 1 & 0 & -\frac{1}{2i} \\ 0 & 1 & \frac{1}{2i} \end{bmatrix} \end{align}\]

    so \(c_1 = -1/(2i) = i/2\) and \(c_2 = 1/(2i) = -i/2\) and

    (6.71)#\[\begin{equation} \vv{y} = \frac{i}{2} e^{4it} \begin{bmatrix} -i \\ 1 \end{bmatrix} - \frac{i}{2} e^{-4it} \begin{bmatrix} i \\ 1 \end{bmatrix} \end{equation}\]

    This solution is acceptable, but we can simplify it further using Euler’s identity:

    (6.72)#\[\begin{align} \vv{y} &= \frac{1}{2} \left( \cos 4t + i \sin 4t \right) \begin{bmatrix} 1 \\ i \end{bmatrix} - \frac{1}{2} \left( \cos 4t - i \sin 4t \right) \begin{bmatrix} -1 \\ i \end{bmatrix} \\ &= \begin{bmatrix} \cos 4t \\ -\sin 4t \end{bmatrix} \end{align}\]

    so

    (6.73)#\[\begin{align} y_1 &= \cos 4 t \\ y_2 &= -\sin 4t \end{align}\]

    The critial point is a center because the eigenvalues are purely imaginary.

  4. For:

    (6.74)#\[\begin{equation} \vv{A} = \begin{bmatrix} 2 & -2\\ 2 & 2 \end{bmatrix} \end{equation}\]
    Solution

    First, find the eigenvalues of A

    (6.75)#\[\begin{align} \vv{A} - \lambda\vv{I} &= \begin{vmatrix} 2- \lambda & -2\\ 2 & 2-\lambda \end{vmatrix} \\ &= (\lambda - 2)^2 + 4 = 0 \\ \lambda_{1,2} &= 2 \pm 2i \end{align}\]

    For \(\lambda_1 = 2+2i\),

    (6.76)#\[\begin{equation} \vv{A}-\lambda_1\vv{I} = \begin{bmatrix} -2 i & -2\\ 2 & -2i \end{bmatrix} \to \vv{x}_1 = \begin{bmatrix} i \\ 1 \end{bmatrix} \end{equation}\]

    For \(\lambda_2 = 2-2i\),

    (6.77)#\[\begin{equation} \vv{A}-\lambda_2\vv{I} = \begin{bmatrix} 2 i & -2\\ 2 & 2i \end{bmatrix} \to \vv{x}_2 = \begin{bmatrix} -i \\ 1\end{bmatrix} \end{equation}\]

    The general solution is:

    (6.78)#\[\begin{align} \vv{y} &= c_1 e^{(2+2i)t} \begin{bmatrix} i\\ 1 \end{bmatrix} + c_2 e^{(2-2i)t} \begin{bmatrix} -i\\ 1 \end{bmatrix} \\ &= e^{2t} \Biggl( c_1 e^{2it} \begin{bmatrix} i\\ 1 \end{bmatrix} + + c_2 e^{-2it} \begin{bmatrix} -i\\ 1 \end{bmatrix}\Biggr) \end{align}\]

    To solve for the initial condition, form the augmented matrix for \(\vv{X}\vv{c} = \vv{y}(0)\),

    (6.79)#\[\begin{align} \begin{bmatrix} i & -i & 1\\ 1 & 1 & 0 \end{bmatrix} \begin{matrix}{\rm swap} \\ \vphantom{R_2}\end{matrix} &\to \begin{bmatrix} 1 & 1 & 0\\ i & -i & 1 \end{bmatrix} \begin{matrix}\vphantom{R_1} \\ -i R_1 \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 0\\ 0 & -2i & 1 \end{bmatrix} \begin{matrix}\vphantom{R_1} \\ \div -2i \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & \frac{-1}{2i} \end{bmatrix} \begin{matrix} -R_2 \\ \vphantom{R_2}\end{matrix} \\ &\to \begin{bmatrix} 1 & 0 & \frac{1}{2i}\\ 0 & 1 & - \frac{1}{2i} \end{bmatrix} \end{align}\]

    so \(c_1 = 1/(2i) = -i/2\) and \(c_2 = -1/(2i) = i/2\). Hence,

    (6.80)#\[\begin{equation} \vv{y} = e^{2t} \Biggl( - \frac{i}{2} e^{2it} \begin{bmatrix} i \\ 1 \end{bmatrix} + \frac{i}{2} e{-2it} \begin{bmatrix} -i\\ 1 \end{bmatrix} \Biggr) \end{equation}\]

    Simplifying using Euler’s identity \(e^{ix} = \cos x + i \sin x\) and adding across the rows gives

    (6.81)#\[\begin{align} y_1 &= e^{2t} \cos 2t\\ y_2 &= e^{2t} \sin 2t \end{align}\]

    The critical point is an unstable spiral because the eigenvalues are complex, and the real part is positive.

Contents