3.2. Systems of linear equations

A system of linear equations has the form:

(3.24)\[\begin{align} a_{11}x_{1} + \cdots + a_{1n}x_{n} &= b_{1} \\ \vdots \\ a_{m1}x_{1} + \cdots + a_{mn}x_{n} &= b_{n} \end{align}\]

There are n unknown variables, \((x_1, \cdots, x_n)\) and m equations. The m equations have coefficients \(a_{mn}\) for each of the n variables and m right-hand side values \((b_1, \cdots, b_m)\). These equations be rewritten using matrices and vectors:

(3.25)\[\begin{equation} \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix} \begin{bmatrix} \ x_{1} \\ \vdots \\ x_{n} \end{bmatrix} = \begin{bmatrix} b_{1} \\ \vdots \\ b_{m} \end{bmatrix} \end{equation}\]

or in shorthand:

(3.26)\[\begin{equation} \vv{A}\vv{x} = \vv{b} \end{equation}\]

A system of linear equations can have:

• No solution (inconsistent equations)

• One solution

• Infinitely many solutions (undetermined)

For example, consider the following graphs of different systems of 2 equations:

• \(x+y = 1\), \(x+y = 0\)

  

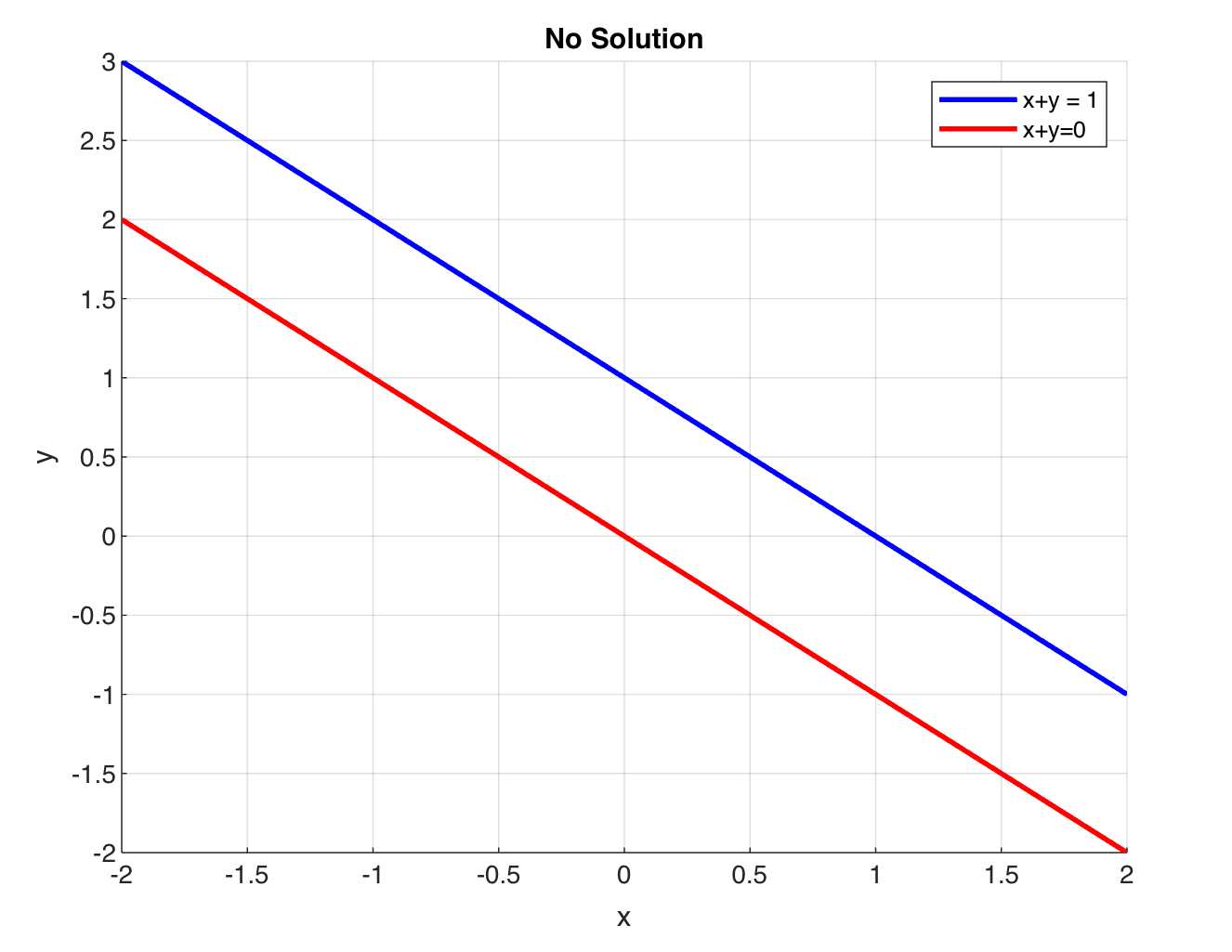
  This system of equations has no solution because the two lines are parallel and never intersect.

• \(x + y = 1\), \(2x - y = 0\)

  

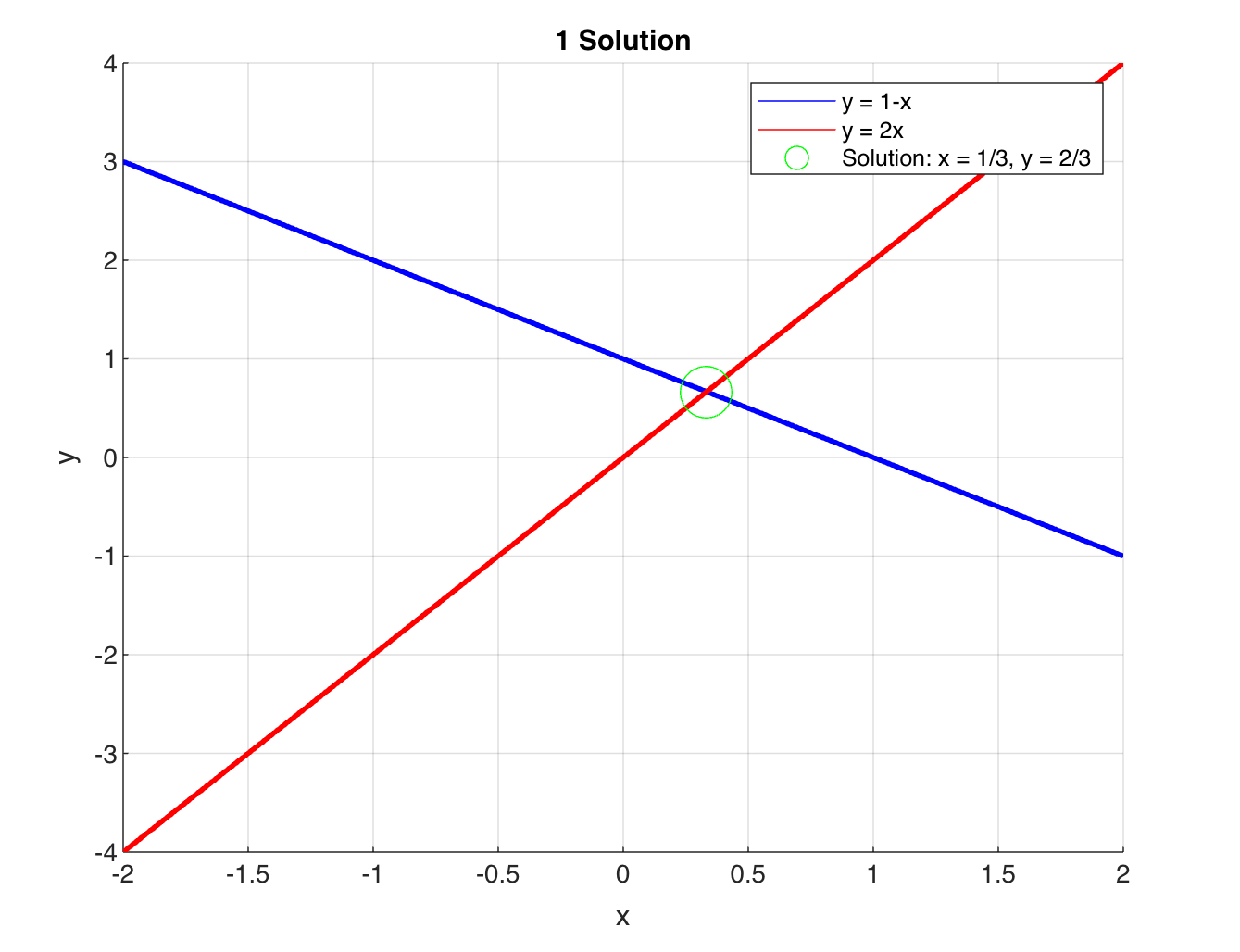
  This system of equations has one solution because the two lines intersect at a point.

• \(x+y = 1\), \(2x + 2y = 2\)

  

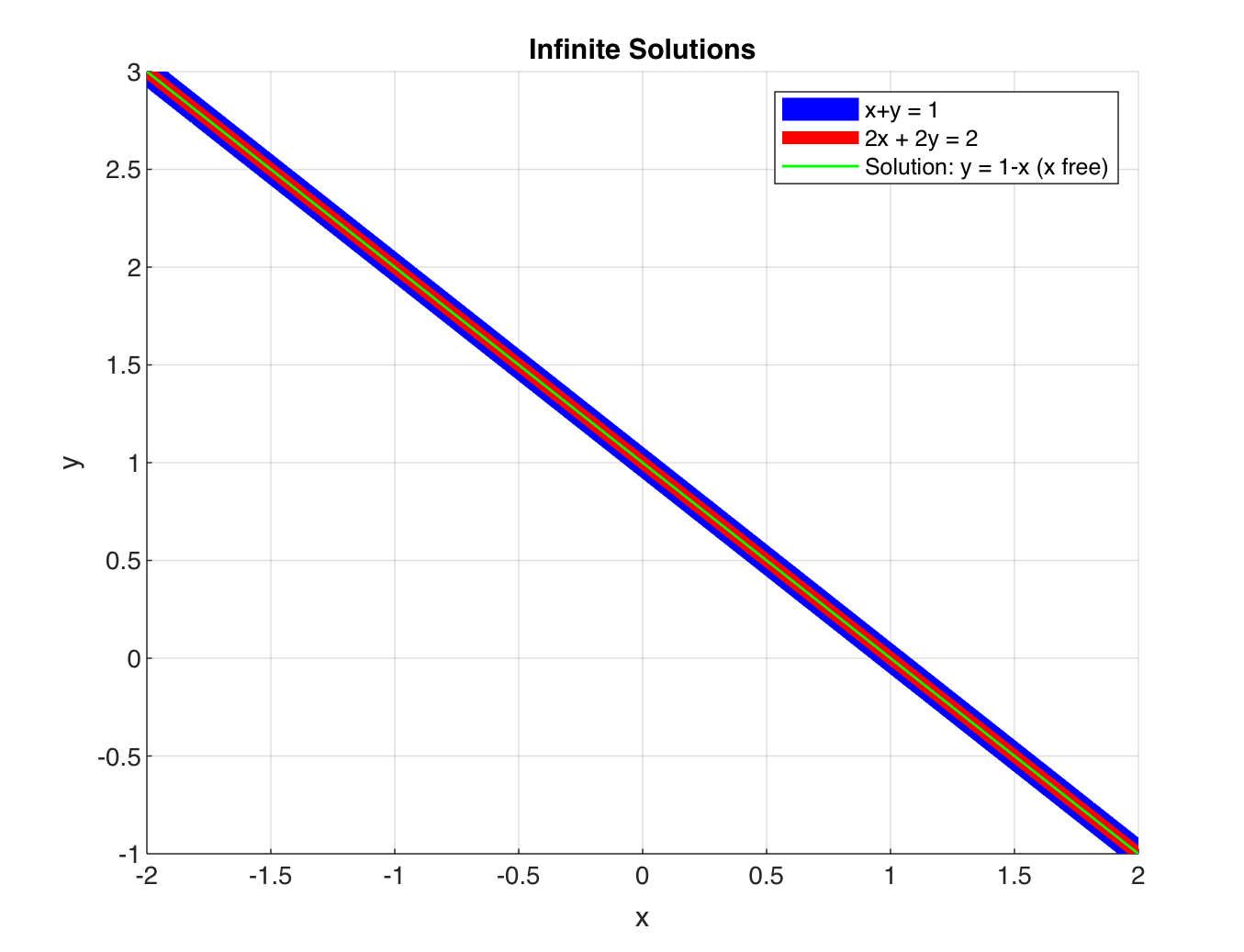
  This system of equations has infinitely many solutions because the two lines are parallel and completely overlap.