Gauss–Jordan elimination

3.3. Gauss–Jordan elimination#

Example: Pump circuit

Incompressible flow can be written analogous to an electrical circuit as

(3.27)#\[\begin{equation} -\Delta P = RQ \end{equation}\]

where \(\Delta P\) is the pressure change, R is the resistance, and Q is the volumetric flow rate. For the following pump “circuit”:

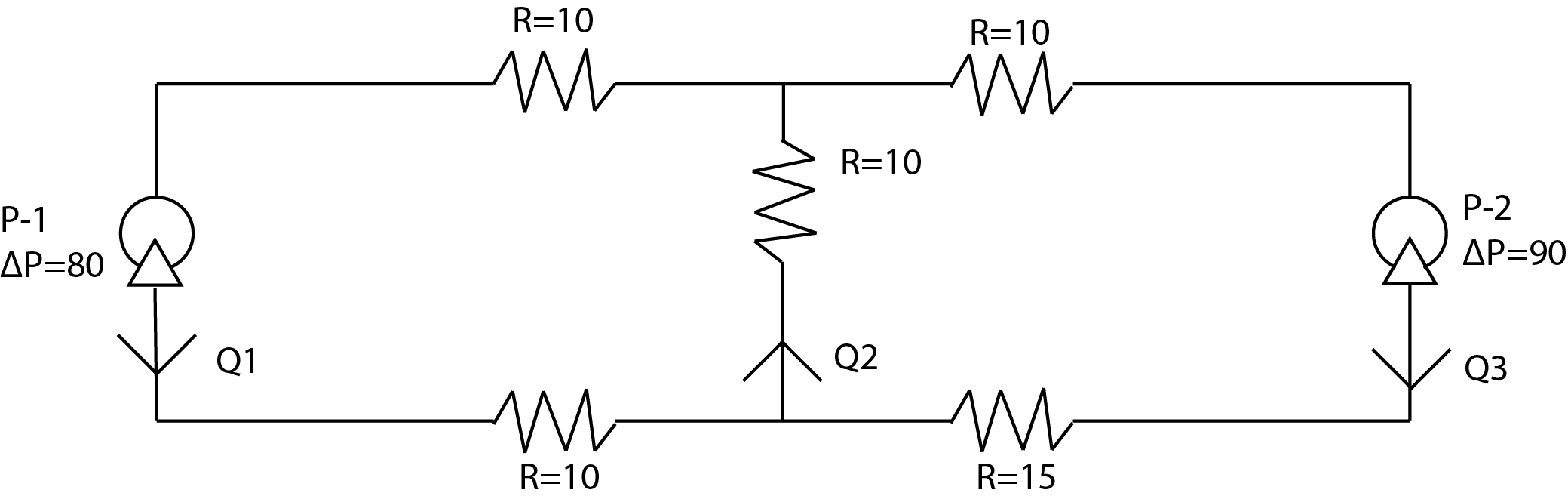
Fluid System Modeled as Circuit

The pressure and mass balances for the nodes and loop give:

(3.28)#\[\begin{align} Q_1 &+ Q_3 = Q_2 \\ Q_2 &= Q_1 + Q_3 \\ 80 &= 10Q_2 + 20Q_1 \\ 90 &= 25Q_3 + 10Q_2 \end{align}\]

Find \(Q_1\), \(Q_2\), and \(Q_3\).

First, rearrange the equations into consistent linear form:

(3.29)#\[\begin{align} Q_1 - Q_2 + Q_3 &= 0 \\ Q_1 - Q_2 + Q_3 &= 0 \\ 20Q_1 + 10Q_2 + 0Q_3 &= 80 \\ 0Q_1 + 10Q_2 + 25Q_3 &= 90 \end{align}\]

Then, rewrite using matrix representation:

(3.30)#\[\begin{equation} \begin{bmatrix} 1 & -1 & 1 \\ 1 & -1 & 1 \\ 20 & 10 & 0 \\ 0 & 10 & 25 \end{bmatrix} \begin{bmatrix} Q_1 \\ Q_2 \\ Q_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 80 \\ 90 \end{bmatrix} \end{equation}\]

Now, perform Gauss-Jordan elimination steps to solve for the unknown flow rates. We form the augmented matrix, then use Row 1 to eliminate values in Rows 2 and 3:

(3.31)#\[\begin{equation} \begin{bmatrix} 1 & -1 & 1 & 0 \\ -1 & 1 & -1 & 0 \\ 20 & 10 & 0 & 80 \\ 0 & 10 & 25 & 90 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ + R_1 \\ -20 R_1 \\ \vphantom{R_1} \end{matrix} \to \begin{bmatrix} 1 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 30 & -20 & 80 \\ 0 & 10 & 25 & 90 \end{bmatrix} \end{equation}\]

Row 2 is all zeros because it was a redundant equation to Row 1. Swap Rows 2 and 4, then use the new Row 2 to eliminate value in Row 3:

(3.32)#\[\begin{equation} \begin{bmatrix} 1 & -1 & 1 & 0 \\ 0 & 10 & 25 & 90 \\ 0 & 30 & -20 & 80 \\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ \vphantom{R_1} \\ -3 R_2 \\ \vphantom{R_1} \end{matrix} \to \begin{bmatrix} 1 & -1 & 1 & 0 \\ 0 & 10 & 25 & 90 \\ 0 & 0 & -95 & -190 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{equation}\]

Normalize Row 3 (divide by -95), then eliminate values above in Column 3:

(3.33)#\[\begin{equation} \begin{bmatrix} 1 & -1 & 1 & 0 \\ 0 & 10 & 25 & 90 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{matrix} - R_3 \\ -25 R_3 \\ \vphantom{R_1} \\ \vphantom{R_1} \end{matrix} \to \begin{bmatrix} 1 & -1 & 0 & -2 \\ 0 & 10 & 0 & 40 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{equation}\]

Normalize Row 2 (divide by 10), then eliminate values above in Column 2:

(3.34)#\[\begin{equation} \begin{bmatrix} 1 & -1 & 0 & -2 \\ 0 & 1 & 0 & 4 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix} \begin{matrix} + R_2 \\ \vphantom{R_1} \\ \vphantom{R_1} \\ \vphantom{R_1} \end{matrix} \to \begin{bmatrix} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 4 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{equation}\]

Turning back into an equivalent system of equations gives the final solution, \(Q_1 = 2\), \(Q_2 = 4\), and \(Q_3 = 2\).

3.3.1. Skill builder problems#

  1. Solve using Gauss-Jordan elimination

    (3.35)#\[\begin{align} 5 x_1 - 2 x_2 &= 20.9 \\ -x_1 + 4x_2 &= -19.3 \end{align}\]
    Solution

    Form the augmented matrix and perform row reduction:

    (3.36)#\[\begin{align} \begin{bmatrix} 5 & -2 & 20.9 \\ -1 & 4 & -19.3 \end{bmatrix} \begin{matrix} {\rm swap} \\ \vphantom{R_2}\end{matrix} &\to \begin{bmatrix} -1 & 4 & -19.3 \\ 5 & -2 & 20.9\end{bmatrix} \begin{matrix} \times -1 \\ \vphantom{R_2}\end{matrix} \\ &\to \begin{bmatrix} 1 & -4 & 19.3 \\ 5 & -2 & 20.9\end{bmatrix} \begin{matrix} \vphantom{R_1} \\ -5 R_1 \end{matrix} \\ &\to \begin{bmatrix} 1 & -4 & 19.3 \\ 0 & 18 & -75.6\end{bmatrix} \begin{matrix} \vphantom{R_1} \\ \div 18 \end{matrix} \\ &\to \begin{bmatrix} 1 & -4 & 19.3 \\ 0 & 1 & -4.2\end{bmatrix} \begin{matrix} +4 R_2 \\ \vphantom{R_2} \end{matrix} \\ &\to \begin{bmatrix} 1 & 0 & 2.5 \\ 0 & 1 & -4.2\end{bmatrix} \end{align}\]

    so \(x_1 = 2.5\) and \(x_2 = -4.2\).

  2. Solve using Gauss-Jordan elimination

    (3.37)#\[\begin{align} x_1 + 4 x_2 = 8 \\ 2 x_1 + 8 x_2 = 17 \end{align}\]
    Solution
    (3.38)#\[\begin{align} \begin{bmatrix} 1 & 4 & 8 \\ 2 & 8 & 17 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ -2 R_1\end{matrix} &\to \begin{bmatrix} 1 & 4 & 8 \\ 0 & 0 & 1\end{bmatrix} \end{align}\]

    The equations do not have a solution because the last row is false.

  3. Solve using Gauss-Jordan elimination

    (3.39)#\[\begin{align} x_1 + x_2 + x_2 = 2 \\ 4x_2 + 6 x_3 = -12 \\ x_1 + x_2 + x_3 = 2 \end{align}\]
    Solution
    (3.40)#\[\begin{align} \begin{bmatrix} 0 & 1 & 1 & -2 \\ 0 & 4 & 6 & -12 \\ 1 & 1 & 1 & 2 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ \rm shuffle \\ \vphantom{R_3} \end{matrix} &\to \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 1 & 1 & -2 \\ 0 & 4 & 6 & -12 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ \vphantom{R_2} \\ \ -4 R_2 \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 1 & 1 & -2 \\ 0 & 0 & 2 & -4 \end{bmatrix} \begin{matrix} \vphantom{R_1} \\ \vphantom{R_2} \\ \div 2 \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 1 & 1 & -2 \\ 0 & 0 & 1 & -2 \end{bmatrix} \begin{matrix} -R_3 \\ -R_3 \\ \vphantom{R_3} \end{matrix} \\ &\to \begin{bmatrix} 1 & 1 & 0 & 4 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -2 \end{bmatrix} \begin{matrix} -R_2 \\ \vphantom{R_2} \\ \vphantom{R_3} \end{matrix} \\ &\to \begin{bmatrix} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -2 \end{bmatrix} \end{align}\]

    so \(x_1 = 4\), \(x_2 = 0\), and \(x_3 = -2\).

Contents