4.1. Quadratic and cubic polynomials

A polynomial of degree \(n\)

(4.1)\[\begin{equation} a_n x^n + \cdots + a_1 x_1 + a_0 = 0 \end{equation}\]

has \(n\) roots, which may be real or complex. Real roots may be distinct or repeated. Complex roots always come in conjugate pairs, \(a \pm bi\), where a is called the real part, \(\pm b\) is called the imaginary part, and \(i = \sqrt{-1}\) is the imaginary unit.

4.1.1. Quadratic polynomials

Quadratic polynomials can have three types of roots:

• Two real roots

• One (repeated) root

• Two complex roots

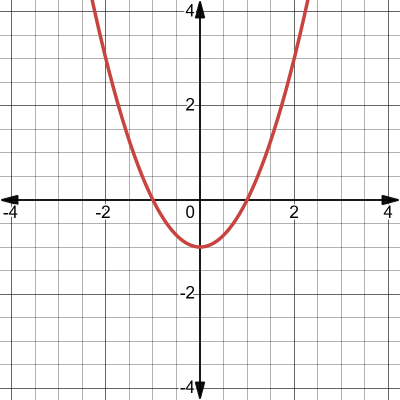
Graphically, two real roots occur as two intersections of a parabola with the y-axis. For example, the roots of \(x^2 - 1 = 0\) occur at \(x = \pm 1\):

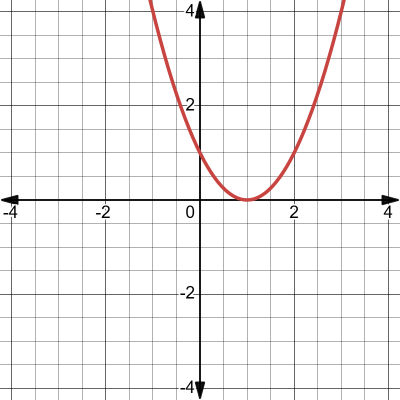
One repeated root occurs as a single point of a parabola (its minimum or maximum) touching the y-axis. For example, the root of \((x-1)^2 = 0\) occurs at \(x = 1\):

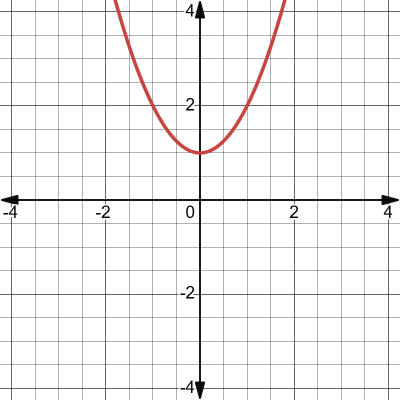
Complex roots do not appear as intersections on a graph. For example, the roots of \(x^2 + 1 = 0\) are \(x = \pm i\):

Example: Complex roots

Find the roots of

(4.2)\[\begin{equation} x^2 - 10x + 34 = 0 \end{equation}\]

---

I will use the technique of completing the square:

(4.3)\[\begin{align} x^2 - 10x &= -34 \\ x^2 - 10x + 25 &= -34 + 25 \\ (x - 5)^2 &= -9 \\ x - 5 &= \pm \sqrt{-9} \\ x &= 5 \pm 3\sqrt{-1} \\ x &= 5 \pm 3i \end{align}\]

4.1.2. Cubic (and higher) polynomials

General formulas for roots of cubic and quartic polynomials are known but complicated. No such formula exists for higher-order polynomials. In these cases, numerical methods are needed!